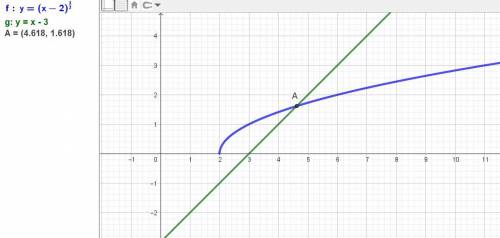
Дано уравнение: √(x - 2) = x - 3.
ОДЗ: х - 2 > 0, x > 2.
Надо обе части уравнения возвести в квадрат.
х - 2 = х² - 6х + 9.
Получаем квадратное уравнение:
х² - 7x + 11 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-7)^2-4*1*11=49-4*11=49-44=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-7))/(2*1)=(√5+7)/2=√5/2+7/2=√5/2+3.5~~4.618034;
x_2=(-√5-(-7))/(2*1)=(-√5+7)/2=-√5/2+7/2=-√5/2+3.5~~2.381966.
Получили 2 корня - это результат лишнего корня при возведении в квадрат, но должна быть одна точка пересечения одной ветви параболы и прямой.
Второй корень не подходит.
ответ: х1 = √5/2+3,5.
Потом спускается на 11
Значит преодолевает так 2 этажа
Поэтапно нужно ехать снова на 13 и на 11 вниз продвигаясь по 2 этажа за раз
То есть мы можем стоять в промежутке между сессиями на четном этаже
Так как в доме 33 этажа это позволяет нам это совершать без проблем до 20 этажа и даже больше. Последний раз стоя на 20-м этаже, мы можем подняться на 13 и окажемся на 33-м
И спустившись на 11-ть окажемся на 22-м
Вот это предел возможностей