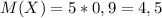 , то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
, то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
Пошаговое объяснение:
Пусть проводится 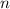 независимых испытаний, даже не обязательно повторных. И в каждом из которых случайное событие
независимых испытаний, даже не обязательно повторных. И в каждом из которых случайное событие 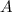 может появиться с вероятностью
может появиться с вероятностью 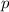 . Тогда случайная величина
. Тогда случайная величина 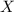 , это число появлений события
, это число появлений события 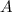 в данной серии испытаний, имеет биномиальное распределение.
в данной серии испытаний, имеет биномиальное распределение.
Кондрат последовательно заходит в 5 автобусов, то есть совершается серия и 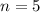 и только 5 похождений в различные автобусы, где вероятность встретить контролера в каждом из них составляет
и только 5 похождений в различные автобусы, где вероятность встретить контролера в каждом из них составляет 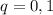 . Тогда вероятность НЕ встретить контролера в автобусе равна
. Тогда вероятность НЕ встретить контролера в автобусе равна 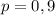 .
.
Математическое ожидание при биномиальном распределении рассчитывается согласно формуле:
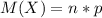 , где
, где 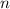 - количество независимых испытаний, то есть количество автобусов, в которое последовательно заходит Кондрат,
- количество независимых испытаний, то есть количество автобусов, в которое последовательно заходит Кондрат, 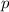 - вероятность появления события
- вероятность появления события 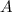 , то есть автобуса без контролера.
, то есть автобуса без контролера.
Найдем математическое ожидание числа автобусов в которые успеет зайти Кондрат:
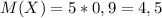 - то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
- то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
(a*b)*c = a*(b*c) - сочетательное свойство умножения.
(a + b) * c = ac + bc - распределительное свойство умножения.
Так же:
1 * a = a
И
1/a * a = 1