1. Как называются числа, задающие положение точки в координатной плоскости?
А) вершинами
Б) целыми
Р) координатами
2. Под каким углом пересекаются координатные прямые х и у, образующие систему координат на плоскости?
А) 60°
Б) 180°
И) 90
3. Сколько чисел надо указать, чтобы задать положение точки на координатной плоскости?
А) 1
С) 2
В) 3
4. Как называется первое из чисел, задающее положение точки на координатной плоскости?
У) абсцисса
Б) ордината
В) аппликата
5. Как называется второе из чисел, задающее положение точки на координатной плоскости?
А) абсцисса
Ю) ордината
В) аппликата
6. В каком координатном углу (четверти) лежит точка С (7; -4)
А) первом
Б) втором
В) третьем
С) четвёртом
7. В каком координатном углу (четверти) лежит точка В (-9; 2)
А) первом
О) втором
В) третьем
Г) четвёртом
8. В каком координатном углу (четверти) лежит точка С (-2; -5)
А) первом
Б) втором
З) третьем
Ю) четвёртом
9. В каком координатном углу (четверти) лежит точка К (7;8)
В) первом
Б) втором
А) третьем
Г) четвёртом
10. На какой оси лежит точка, имеющая координаты (0; -2)
А) Ох
Е) Оу
Ж) не знаю
11. На какой оси лежит точка, имеющая координаты (3;0)
З) Ох
Б) Оу
К) не знаю
12. Какая запись соответствует условию: точка М с абсциссой -2 и ординатой 9
А) М (9; -2)
Д) М (-2; 9)
Л) М (2;9)
13. Что общего имеют все точки, лежащие на оси абсцисс?
А) их абсцисса равна нулю
И) их ордината равна нулю
К) совпадают
14. Что общего имеют все точки, лежащие на оси ординат?
Е) Совпадают
Я) их абсцисса равна нулю
Б) их ордината равна нулю
Пошаговое объяснение:
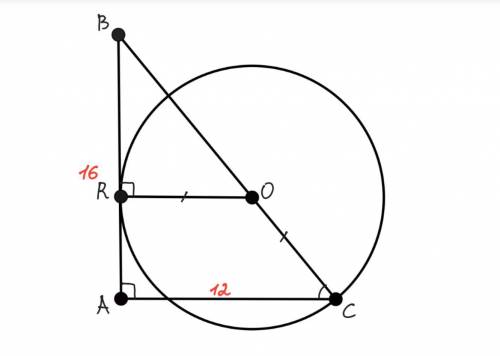
Дано: ΔABC — прямокутний, АВ і АС — катети, АВ=16 см, АС=12 см, коло(R;OC), т.О∈ВС, т.R — точка дотику кола до ΔАВС, т.R∈AB.
Знайти: радіус R кола.
Розв'язання.
1) Знайдемо гіпотенузу ВС ΔАВС за т.Піфагора:
АВ²+АС²=ВС²;
16²+12²=ВС²;
ВС²= 256+144;
ВС²= 400;
ВС= 20 см (–20 не задовольняє умові)
2) Проведемо радіус OR. R=OR=OC. Оскільки т.R — точка дотику, то OR⟂АВ.
3) Оскільки OR⟂AB і AB⟂AC (катети перпендикулярні), то OR||AC і трикутники ΔАВС і ΔRBO подібні за лемою.
(Лема про подібні трикутники: пряма, паралельна стороні трикутника, відтинає від нього трикутник, подібний даному)
4) ΔАВС подібний ΔRBO. Це означає, що відповідні сторони цих трикутників відносяться.
А тому справедливою буде така рівність:
АС/OR=BC/BO.
Нехай OR=OC=R (радіус, який потрібно знайти). Тоді ВО=ВС–ОС=ВС–R=20–R.
AC / R=BC / (BC–R);
12 / R= 20 / (20–R); (по пропорции решаем)
12(20–R)=20R;
240–12R=20R;
240=32R;
R= 240/32;
R= 15/2;
R= 7,5 (см)
Відповідь: 7,5 см.
ответ Б.