Если я правильно понял задание, то требуется посчитать:
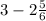 .
.
Числитель - верхнее число в дроби.
Знаменатель - нижнее число в дроби.
В таком случае, следует 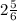 перевести в неправильную дробь (2 умножить на знаменатель и прибавить числитель. Затем полученное число записать в числитель, оставив знаменатель неизменным).
перевести в неправильную дробь (2 умножить на знаменатель и прибавить числитель. Затем полученное число записать в числитель, оставив знаменатель неизменным).
Получится: 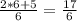
Затем представим 3 в виде неправильной дроби со знаменателем 6 (3 умножим на знаменатель и полученное число поставим на место числителя, оставив знаменатель неизменным).
Получится: 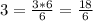
Теперь посчитаем полученные дроби (считаем только числители при одинаковых знаменателях, оставляя сам знаменатель неизменным):
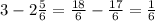
ответ: 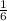 .
.
Число 5АА это может быть число 511, 522, 533 и т.д. вплоть до 599. Из этих чисел мы должны выбрать такое, что если из него вычесть 8, то результат должен делиться на 9 без остатка. То есть, воспользовавшись признаком делимости на 9 (сумма цифр числа должна быть кратна 9) приходим к такому условию:
Выражение (5 + а + а - 8) должно делиться на 9 без остатка
Решим уравнение: 5+2а-8=9, получим, что а = 6.
Тогда проверяем число 566. 566:9 = 62 (ост. 8)
Итак: делимое 566, делитель 9, частное 62.