Question

Найдите наименьшее значение функции y=(x^2-39x+39)*e^(2-x) на отрезке [ 0; 6]. зарание .

Answer 1

Решение:

Сначала найдем производную функции:

    $\displaystyle \Big ( y \Big )' = \Big ( (x^2-39x+39) \cdot e^{2-x} \Big ) ' = \\\\\\= \Big ( x^2-39x+39 \Big ) ' \cdot e^{2-x} + \Big (e^{2-x} \Big ) ' \cdot (x^2-39x+39) = \\\\\\= \Big ( 2x - 39 \Big ) \cdot e^{2-x} +\Big ( (-1) \cdot e^{2-x} \Big ) \cdot (x^2 - 39x + 39) = \\\\\\= e^{2-x} \cdot \Big ( (2x-39)-(x^2-39x+39) \Big ) = \\\\\\= e^{2-x} \cdot (-x^2 + 41x - 78)$

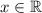Также заметим, что функция, как и производная, определена для всех значений $x$ (иначе говоря, $x \in \mathbb R$). Теперь, чтобы найти критические точки производной, приравняем ее к нолю:

    $e^{2-x} \cdot (-x^2 + 41x - 78) = 0$

Сразу же заметим, что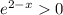 $e^{2-x} 0$, поэтому обе части можно разделить на данное выражение:

    $-x^2 + 41x - 78 = 0 \;\;\; \Big | \cdot (-1) \\\\x^2 - 41x + 78 = 0$

Дальше воспользуемся теоремой Виета:

    $\displaystyle \left \{ {{x_1+x_2=41} \atop {x_1 \cdot x_2=78}} \right. ; \;\;\; \Rightarrow \;\;\; \left \{ {{x_1=2} \atop {x_2=39}} \right.$

Полученные две точки выставим на координатной прямой, а потом на получившихся трех промежутках расставим знаки производной:

          - - -                 + + +                    - - -

    ________$\Big ( \; 2 \; \Big )$________$\Big ( \; 39 \; \Big )$________$\rightarrow x$

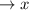
Можно сделать вывод, что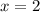 $x=2$ - точка минимума функции (в силу того, что знак меняется с «-» на «+»), а 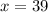$x=39$ - точка максимума (так как происходит смена знака с «+» на «-»).

Дальше остается заметить, что единственная точка минимума функции (как мы ранее получили,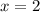 $x=2$) располагается на заданном в условии отрезке $\Big [ 0; 6 \Big ]$.

Эта точка также будет соответствовать ответу, так как на промежутке $[0;2]$ функция убывает, а на промежутке $[2;6]$ - возрастает:

                  ↘                    ↗

     $\Big ( \; 0 \; \Big )$_______$\Big ( \; 2 \; \Big )$_______$\Big ( \; 6 \; \Big )$

Точку, соответствующую ответу, мы нашли. Осталось только определить значение функции в этой точке:

    $y(2) = (2^2-39 \cdot 2+39) \cdot e^{2-2} = (4 - 39) \cdot 1 = \underbrace { \; -35 \; } _{\text{min} \;y}$

Задача решена!

ответ: - 35 .