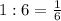часть поля вспашут вместе за 1час
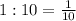часть поля вспашет первый тракторист за 1 час
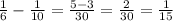часть поля вспашет второй тракторист за 1час
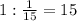ч-время за которое вспашет поле второй тракторист
Возьмём производную. Если производная в данной точке больше 0, функция растёт и наоборот.
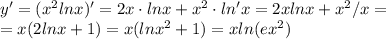
Если подлогарифмическое выражение больше 1, то логарифм больше единицы.
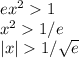
Если логарифм больше 0, то при отрицательных х производная меньше 0 (x<-1/sqrt(e)), при положительных - больше 0 (x>1/sqrt(e)).
Если логарифм меньше 0 (|x|<1/sqrt(e)), то при положительных х производная меньше 0 (0<x<1/sqrt(e)), при отрицательных - больше 0 (-1/sqrt(e)<x<0)
В крайних точках функция определена (кроме х=0), значит интервалы включают крайние значения.
Функция убывает при ![x\epsilon(-\infty;-1/\sqrt{e}]\cup(0;1/\sqrt{e}]](/tpl/images/0150/0553/0bd51.png)
Возрастает при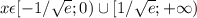 
аb+bc+ca=5abc
x=a+b+c (1)
Нужно найти min{x}.
1. Если бы числа a, b, c были по условию целые, то:
(аb+bc+ca)/abc=5
1/c+1/a+1/b=5
Из последнего видно, что не существует таких целых чисел. Минимальные положительные значения a, b, c, чтобы 1/c+1/a+1/b - было целым числом равны 1, но сумма их равна 3. Значит они должны быть меньше 1, но больше 1/5.
2. Найдем экстремум функции 2-х переменных.
Из системы (1) выразим с и х, получим:
5ab-a-b!=0, c =(ab)/(5ab-a-b), x =(5a^2b-a^2+5ab^2-ab-b^2)/(5ab-a-b), ab!=0 (!= - не равно)
Найдем частные производные первого порядка.
x =(5a^2b-a^2+5ab^2-ab-b^2)/(5ab-a-b)
(dx(a,b))/(da) = (a^2+2ab-10a^2b-10ab^2+25a^2b^2)/(-a-b+5ab)^2
(dx(a,b))/(db) = ((-1+5a)b(-b+a(-2+5b)))/(a+b-5ab)^2
Найдем стационарные точки решая с-му уравнений:
(a^2+2ab-10a^2b-10ab^2+25a^2b^2)/(-a-b+5ab)^2=0
(dx(a,b))/(db) = ((-1+5a)b(-b+a(-2+5b)))/(a+b-5ab)^2=0
(потрудитесь сами)
Получатся некие точки: M1(...), M2(...),...
Отбираем только те, которые соответствуют условию, что a>0, b>0, c>0. и условию 1/c+1/a+1/b=5 -> 1<a<1/5, 1<b<1/5, 1<c<1/5.
Найдем частные производные второго порядка:
(d^2x(a,b))/(da^2) = (2(-b^2+5b^3))/(-a-b+5ab)^3
(d^2x(a,b))/(da db) = (2ab)/(-a-b+5ab)^3
(d^2x(a,b))/(db^2) = (2(-a^2+5a^3))/(-a-b+5ab)^3
Найдем значения этих производных в т.Mn, если точка Mn не одна, находим все значения.
Найдем Δ=AC-B^2, где
A=f''aa(a0;b0)=(d^2x(a,b))/(da^2), В=ƒ''ab(a0;b0)=(d^2x(a,b))/(da db), С=ƒ''bb(a0;b0)=(d^2x(a,b))/(db^2).
(самостоятельно)
Получим некие значения Δ (если Мn одна, то значение одно)
Возможны такие варианты:
1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А < 0; минимум, если А > 0;
2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.
В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования.
(в одном из решений должно получиться Δ > 0 и А > 0)
(все решаем самостоятельно)
После всего координаты т. Мn, в которой Δ > 0 и А > 0 подставляем в
x =(5a^2b-a^2+5ab^2-ab-b^2)/(5ab-a-b) и находим минимальное значение суммы чисел а,b и с.
Помимо всего, у нас еще и значеня самих а, b и с получатся а и b это координаты т. Мn (3/5,3/5), которая удовлетворяет условию Δ > 0 и А > 0, а значение с найдем из c =(ab)/(5ab-a-b).
ответ:
min{x =(5a^2b-a^2+5ab^2-ab-b^2)/(5ab-a-b)} = 9/5 при (a,b) =(3/5, 3/5) и с=3/5.
Все.
Проще я не знаю как.
