1) посчитаем, сколько вариантов поставить короля и ферзя:
* они занимают две подряд идущие клетки, всего вариантов 7
* мы можем еще поменять в каждом варианте КФ на ФК, получим еще 7 вариантов
итого 7+7 = 14 вариантов расстановки короля и ферзя
2) осталось шесть клеток (3 белые, 3 черные), поставим слонов:
* выберем любой цвет - 2 варианта
* выберем две клетки из трех - 3 варианта
итого 2*3 = 6 вариантов поставить слонов
3) поставим двух коней
* кони не отличаются, т.к. оба белые
* выберем из оставшихся четырех клеток две: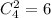 
итого 6 вариантов расставить коней
4) поставим ладьи в оставшиеся клетки
итого 1 вариант для ладей
в итоге для расстановки всех фигур получим:
ответ
Найдем максимальное количество одинаковых чисел.
Рассмотрим любое число на доске. Для данной суммы числа с его последними тремя цифрами существует не более одной подобной суммы, но уже с другим числом. Иначе говоря, ![1000a+100b+10c+d+[100b+10c+d]=1000m+100n+10k+l+[100n+10k+l], \;\; 0\leq b,c,d,n,k,l\leq 9, \;\;0](/tpl/images/0922/2237/a86dd.png)
- имеет единственное решение для данных чисел a,b,c,d; Пусть это выполняется для чисел на доске. Теперь рассмотрим числа в тетради. Из вышесказанного следует, что эти 88 чисел можно разбить определенным образом на 44 пары, где в каждой паре будет два одинаковых числа. То есть может получиться 44 одинаковых числа. Но это с одной стороны. Рассмотрим другую сторону. Заметим, что сумма всех чисел нечетна - 999 999. Следовательно, в этой сумме есть хотя бы одно нечетное число. Взглянем на сумму числа с его тремя последними цифрами: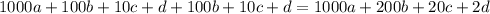 
; Если число четное, то d - четно, значит результат делится на 4. Если d - нечетно, то результат не делится на 4. Раз существует хотя бы одно нечетное число, то рассмотрим одну из 44-ех пар, где четное и нечетное число. В самом начале мы сказали, что в 44 парах равные числа. Но из вышесказанного следует противоречие - сумма четного числа с его последними тремя цифрами не может равняться сумме некоего нечетного числа с его последними тремя цифрами, поскольку последнее не делится на 4, в отличие от четного. Это означает, что хотя бы одна пара будет содержать разные числа. То есть максимальное количество одинаковых чисел равно 44-1=43. А минимальное количество различных чисел равно 88-43 = 45. Значит всегда найдется по крайней мере 45 различных чисел.
1) окружность, зеленая
2) эллипс, красная
3) параболы (2 ветви), фиолетовые