Таблица плотности водно-спиртовых растворов найдена в интернетах
Плотность 40% раствора при 20°С ρ₁= 0,9352 г/мл
Массовая доля спирта при этом η₁ = 374,1 г/л
Плотность 20% раствора при 20°С ρ₂= 0,9686 г/мл
Массовая доля спирта при этом η₂ = 193,7 г/л
Плотность воды при 20°С ρ₀ = 998,2 г/мл
1. Масса исходного раствора
m₁ = V₁*ρ₁ = 20*1000*0,9352 = 18704 грамма
2. Масса спирта в исходном растворе
z = V₁*η₁ = 20*374,1 = 7482 грамма
3. Объём целевого раствора по известной массе спирта
z = V₂*η₂
V₂ = z/η₂ = 7482/193,7 = 38,627 литров
4. Масса целевого раствора
m₂ = V₂*ρ₂ = 38,627*1000*0,9686 = 37414 грамм
5. масса добавленной воды
m₀ = m₂-m₁ = 37414 - 18704 = 18710 грамм
6. объём добавленной воды
m₀ = V₀*ρ₀
V₀ = m₀/ρ₀
V₀ = 18710/998,2 = 18744 мл = 18,744 л
А теперь как в шестом классе
Все проценты считаются массовыми, и 1 литр раствора или воды всегда весит 1 килограмм :)Изначально было в растворе спирта
20 (кг) * 40%/100% = 8 кг (или можно писать литров, на такие мелочи внимания не обращаем)
И желанная пропорция
в 1 литре целевого раствора 200 грамм спирта
в x литров целевого раствора 8000 грамм спирта
x = 8000*1/200 = 40 литров
Стало 40 литров, было 20, значит надо добавить
V = 40-20 = 20 литров воды
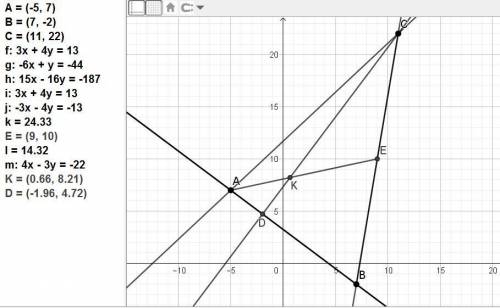
.Даны координаты вершин треугольника АВС А(-5;7) В(7;-2) С(11;22).
Найти:
1) длину стороны АВ = √((7-(-5))² + (-2-7)²) = √(144 + 81) = √225 = 15.
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
к(АВ) = Δу/Δх = -9/12 = -3/4.
к(ВС) = Δу/Δх = 24/4 = 6.
Уравнение АВ: (х + 5)/12= (у - 7)/(-9) каноническое.
Или с угловым коэффициентом: у = (-3/4)х + С. Для определения С подставим координаты точки А: 7 = (-3/4)*(-5) + С, отсюда С = 7-(15/4) =
= 13/4. Уравнение: у = (-3/4)х + (13/4).
Уравнение ВС: (х - 7)/4= (у + 72)/24 каноническое.
Или с угловым коэффициентом: у = 6х + С. Для определения С подставим координаты точки АВ: -2 = 6*7 + С, отсюда С = -2 - 42 =
= -44. Уравнение: у = 6х - 44.
3) угол В в радианах с точностью до двух знаков;
Он между векторами: ВА(-12; 9), его модуль равен √(144 + 81) = 15.
и ВС(4; 24), его модуль равен √(16 + 576) = √592 = 4√37.
cos B = (-12*4 + 9*24)/(15*4√37) = 0,460317164.
Угол B = 1,092443895 радиан или 62,59242456 градусов.
4) уравнение высоты CD и ее длину;
Из пункта 2) находим общее уравнение стороны АВ:
3х + 4у - 13 = 0. Для СD коэффициенты В и А уравнения меняются на -В и А: -4х + 3у + С = 0. Подставляем координаты точки С:
-4*11 + 3*22 + С = 0, отсюда С = 44 - 66 = - 22.
Уравнение СД: -4х + 3у - 22 = 0 или 4х - 3у + 22 = 0.
5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СD;
Точка Е = (В+С)/2 = (9; 10). Вектор АЕ = (9+5; 10-7) = (14; 3).
Уравнение АЕ: (х + 5)/14 = (у - 7)/3 или в общем виде 3х - 14у + 113 = 0.
Точка пересечения с СД находится решением системы:
{4х - 3у + 22 = 0, | x(-3) = -12x + 9y - 66 = 0
{3х - 14у + 113 = 0 | x(4) = 12x - 56y + 452 = 0
-47y + 386 = 0, y = -386/(-47) = 8,2128.
x = (14y - 113)/3 = 31/47 = 0,6596.
6) уравнение прямой, проходящей через точку К параллельно стороне АВ.
Угловой коэффициент этой прямой равен коэффициенту АВ.
Уравнение КР: у = (-3/4) + в, для определения в подставим координаты точки К: 8,9767 = (-3/4)*1,2326 + в, отсюда в = 9,90116.
Уравнение КР: у = (-3/4)х + 9,90116.
a(t)=v`(t)=2*cos2t=1
cos2t=1/2
2t=+/-π/3+2πk
t=+-π/6+πk t≥0
t=π/6+πk