17
Пошаговое объяснение:
Так как правая часть представляет собой результат вычитания, связанный только с функцией f(x) (причём f(x) взята два раза, а f(-x) — только один), никаких элементарных функций, как 2ˣ, ㏒₂x, синус и т. д., кроме представленных в левой части, появиться не могло. Значит, f(x) имеет вид 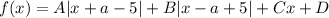 .
.
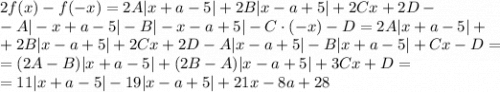
Коэффициенты соответственно равны, следовательно:
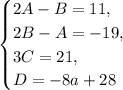
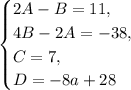
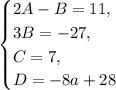
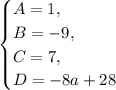
Таким образом, функция равна
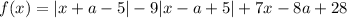
График такой функции — ломаная, поскольку при разном раскрытии модулей изменяется коэффициент перед x и свободный член (функция также непрерывная, поскольку при нулевых значениях модуля значения равны как при одном раскрытии, так и при другом).
Заметим, что при x < a - 5 минимальное значение коэффициента перед x равно -1 + 9 + 7 = -1 (первый модуль раскрыли с минусом для достижения минимальности, второй — с минусом по неравенству), то есть функция на данном промежутке возрастает. При x > a - 5 максимальное значение коэффициента перед x равно 1 - 9 + 7 = -1 (первый модуль — с плюсом, второй — с плюсом по аналогичным причинам), то есть функция убывает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции не больше 0, то при любом другом x значение функции не превышает 0. Значит, достаточно решить неравенство 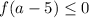 :
:
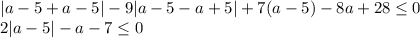
Если a ≥ 5:
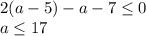
Учитывая ограничение, 5 ≤ a ≤ 17.
Если a < 5:
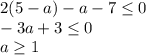
Учитывая ограничение, 1 ≤ a < 5.
Таким образом, 1 ≤ a ≤ 17. Максимальное значение параметра равно 17.
2)7,1+5*(3,4-х)=7,1+17-5х=24,1-5х
3)1,2*(у+5)-1,7=1,2у+6-1,7=1,2у+4,3
4)3х+2,5*(х-6)=3х+2,5х-15=5,5х-15