1) 3 2
8 5 = 3*5 - 2*8 = 15 - 16 = -1.
2) 4 2 -1| 4 2
5 3 -2| 5 3
3 2 -1| 3 2 = -12 - 12 - 10 + 10 + 16 + 9 = 1.
3) x y z B -1 Определитель
1 -1 1 0
2 1 1 5
0 2 -1 3
Заменяем 1-й столбец на вектор результатов B:
0 -1 1 -1 Определитель
5 1 1
3 2 -1
Заменяем 2-й столбец на вектор результатов B:
1 0 1 -2 Определитель
2 5 1
0 3 -1
Заменяем 3-й столбец на вектор результатов B:
1 -1 0 -1 Определитель
2 1 5
0 2 3
x = -1 / -1 = 1
y = -2 / -1 = 2
z = -1 / -1 = 1.
2. Угол при основании равнобедренного треугольника АВС равен 32º, АВ -его боковая сторона, АМ- биссектриса треугольника. Найдите углы треугольника АВМ. (Рассмотрите два случая.)
1) ∠В=180º - 32º*2 = 116º
Так как АМ – биссектриса ∠ВАМ=32:2=16º
∠АМВ=180 – 116-16=48º
2) Из Δ АМС ∠ АМС= 180 – 32-16= 132º
∠АМВ и ∠АМС смежные, значит ∠АМВ=180-132=48º
∠В= 180º- ∠ВАМ -∠АМВ =180-48-16=116º
3. К прямой т проведены перпендикуляры АВ и СD. Докажите, что ∆ АВD=∆ CDB, если AD = BC.
АВ и СD перпендикуляры, значит ∠ ВDС и ∠ АВD =90 º . В четырехугольнике АВDС два угла прямоугольные, а диагонали равны AD = BC. Значит АВDС – прямоугольник. У прямоугольника противоположные стороны равны.
АВ=СD , AD = BC, ВD – общая сторона.
∆ АВD=∆ CDB по трем равным сторонам.
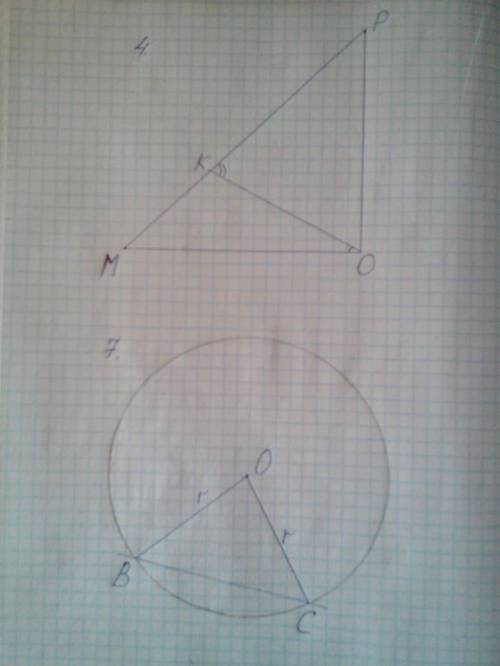
4. В равнобедренном прямоугольном треугольнике MOP на гипотенузе МP отмечена точка К. Известно, что ∠OKP в 4 раза больше, чем ∠МОК. Найдите углы треугольника МОК.
Δ МОК прямоугольный равнобедренный.
∠М=∠Р = 90º:2=45º
∠ОКР=4*∠МОК
Из теоремы о внешних углах ∠М= ∠ОКР-∠МОК
∠М= 4*∠МОК-∠МОК=3∠МОК
∠МОК = 45º:3=15º
∠ МКО=180º - 45º -15º = 120º
Или ∠МКО= 180º - 4*15º=120º
7. В окружности с центром О проведена хорда ВС. Найдите ∠OВС и ∠ВOС, если один из них на 36 º больше другого.
Δ ОВС равнобедренный ВО=ОС= r , значит прилежащие к основанию углы равны.
∠OВС=∠OСВ =хº
2х+х+36 =180
3х = 144
х = 48
∠OВС=∠OСВ =48º
∠ВOС= 48º+36º=84º

2)276:3=92(стр) в 3 книге
ответ: в 3 книге 92 страницы