Сравнить двух учеников с яблоком и книгой . формулировать выводы на основе этой работы

👇

Ответ:

Полиняша

28.06.2022

Первый ученик с яблоком явно глупее чем ученик с книгой ведь если второй повторяет заданное то парень с яблоком ест не пытаясь повысить знания прочтением книги если не правильно отпишы я изменю у меня много версий

4,6(73 оценок)

Открыть все ответы

Ответ:

Ира2806

28.06.2022

Перепишем уравнения в цилиндрической системе координат: (x, y, z) меняются на (r, φ, z) по формулам x = r cos(φ - arctg 3/4), y = r sin(φ - arctg 3/4) – арктангенс возник из соображений удобства, чтобы третье уравнение выглядело поприличнее. Откуда отсчитывать углы, для нас не принципиально.

Первое уравнение:
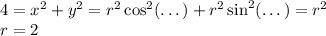
$4=x^2+y^2=r^2\cos^2(\dots)+r^2\sin^2(\dots)=r^2\\
r=2$

Второе уравнение не меняется.

Третье уравнение:
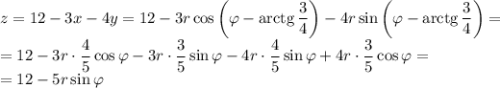
$z=12-3x-4y=12-3r\cos\left(\varphi-\mathop{\mathrm{arctg}}\dfrac34\right)-4r\sin\left(\varphi-\mathop{\mathrm{arctg}}\dfrac34\right)=\\=12-3r\cdot\dfrac45\cos\varphi-3r\cdot\dfrac35\sin\varphi-4r\cdot\dfrac45\sin\varphi+4r\cdot\dfrac35\cos\varphi=\\=12-5r\sin\varphi$

Итак, уравнения поверхностей, ограничивающих тело, выписаны выше: r = 2, z = 1, z = 12 - 5r sin φ. Тело, которое они ограничивают, изображено на приложенном рисунке: это часть цилиндра, вырезанная двумя плоскостями.

Сформулируем условия в виде неравенств.
1 ≤ z ≤ 12 - 5r sin φ
0 ≤ φ ≤ 2π
0 ≤ r ≤ 2

Осталось вспомнить, что элемент объёма в цилиндрических координатах есть dV = r dr dφ dz, и вычислить интеграл:
$\displaystyle \iiint_VdV=\int_0^{2\pi}d\varphi\int_0^2r\,dr\int_1^{12-5r\sin\varphi}dz=\\=\int_0^{2\pi}d\varphi\int_0^2(11-5r\sin\varphi)r\,dr=2\pi\cdot22=44\pi$

ответ: 44π.

________________________________________

Для самопроверки получим этот ответ без интеграла.
Самая нижняя точка, в которой наклонная плоскость пересекает цилиндр, это z = 12 - 5 * 2 = 2, самая высокая – z = 12 + 5 * 2 = 22. Тогда объём равен сумме объёма цилиндра с высотой 2 - 1 = 1 и половины объёма цилиндра с высотой 22 - 2 = 20.
V = S * (h1 + h2 / 2) = 4π * (1 + 10) = 44π
Стройного интеграла вычислить объем тела, ограниченного заданными поверхностями.

Стройного интеграла вычислить объем тела, ограниченного заданными поверхностями.

4,7(89 оценок)

Ответ:

Adidasler05

28.06.2022

Большая сторона первоначального прямоугольника x.

Есть два возможный варианта: 1) прямоугольник разрезали по меньшей стороне; 2) прямоугольник разрезали по большей стороне. Рассмотрим их оба:

1) пусть одна сторона первого прямоугольника y, тогда вторая 6-y. Вторые стороны у обоих x.

Площади: xy кв.ед. у первого, x·(6-y) кв.ед. у второго. У первого в 3 раза больше:

xy = 3x·(6-y)

Периметры: (x+y)·2 у первого, (x+6-y)·2 у второго. У первого в 2 раза больше:

(x+y)·2 = 2·(x+6-y)·2

Составим и решим систему уравнений:

$\begin{cases}\not xy=3\not x\cdot(6-y)\\(x+y)\cdot\not2=2\cdot(x+6-y)\cdot\not2\end{cases}\Rightarrow\begin{cases}y=18-3y\\x+y=2x+12-2y\end{cases}\Rightarrow\\\\\Rightarrow\begin{cases}4y=18\\x=3y-12\end{cases}\Rightarrow\begin{cases}y=4,5\\x=1,5\end{cases}$

Большая сторона первоначального прямоугольника 1,5.

2) пусть одна сторона первого прямоугольника y, тогда вторая x-y. Вторые стороны у обоих 6.

Площади: 6y кв.ед. у первого, 6(x-y) кв.ед. у второго. У первого в 3 раза больше:

6y = 3·6(x-y)

Периметры: у первого (y+6)·2, у второго (x-y+6)·2, у первого в 2 раза больше:

(y+6)·2 = 2·(x-y+6)·2.

Составим и решим систему уравнений:

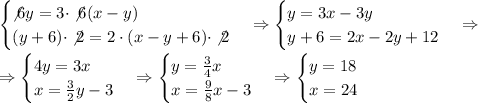
$\begin{cases}\not6y=3\cdot\not6(x-y)\\(y+6)\cdot\not2=2\cdot(x-y+6)\cdot\not2\end{cases}\Rightarrow\begin{cases}y=3x-3y\\y+6=2x-2y+12\end{cases}\Rightarrow\\\\\Rightarrow\begin{cases}4y=3x\\x=\frac32y-3\end{cases}\Rightarrow\begin{cases}y=\frac34x\\x=\frac98x-3\end{cases}\Rightarrow\begin{cases}y=18\\x=24\end{cases}$