BDТЕСТ «ХАН ТАУКЕ»
1. Свод норм обычного права хана Тауке:
А) Пять установлений В) Законы Казахского ханства С) Степные законы Д) Адат Е) «Жеты Жаргы»
2. Свод законов «Жеты Жаргы» были составлены при хане:
А) Хакназаре В) Касыме С) Тауекеле Д)Тауке
Е) Бурундуке
3. Став ханом, Тауке стремился:
А) создать сильное централизованное государство
В) расширить территорию Казахского ханства
С) упрочить казахско-русские дипломатические отношения
Д) покорить Джунгарское ханство
Е) возродить Великий Шелковый путь
4. Верховная власть в Казахском ханстве принадлежала:
А) хану В) гуньмо С) хунтайджи Д)кагану
Е) султану
5. В период правления Тауке:
А) принимается подданство России
В) относительно стабилизируется политическое положение в стране С) издается свод законов «Казахская правда»
Д) устанавливаются дипломатические отношения с Джунгарским ханством
Е)происходит разделение ханства на три жуза
6. Высшее аристократическое сословие казахского общества:
А) кулы В)райаты С) ак-сүйек Д) кара-сүйек Е) шаруа
7. В начале XVIIв. во внутриполитическом положении Казахского государства происходят изменения:
А) «кара суеки» допускаются к власти
В) концентрируется власть
С) усилились феодальные междоусобицы
Д) начинается классовая борьба
Е) чингизиды отстраняются от власти
8. К правовой ответственности по «Жеты -Жаргы» привлекали с:
А) 10 лет В) 13 лет С) 24 лет Д) 18 лет Е) 16 лет
9. Главы родов и племен согласно «Жеты жаргы» должны были являться на народное собрание с:
А) предложениями по политической стабилизации В) оружием
С) дополнениями к своду законов д) податями Е) отчетом
10. 1680-1715годы правления хана:
А) Тауекеля В) Жангира С) Тауке Д) Хакназара Е) Есима
ответ будет дпаае вот тек вот
Пошаговое объяснение:
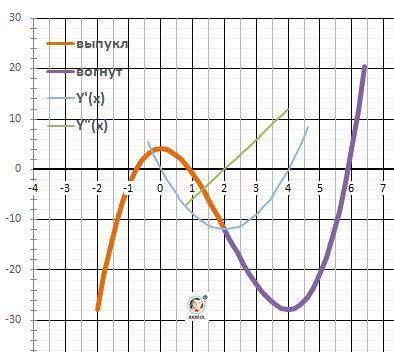
ДАНО:Y(x) = x³ -6*x² +4.
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Вертикальная асимптота - нет - нет разрывов.
3. Наклонная асимптота - y = k*x+b.
k = lim(+∞) Y(x)/x = +∞ - нет наклонной (горизонтальной) асимптоты.
4. Периода - нет - не тригонометрическая функция.
5. Пересечение с осью OХ.
Применим тригонометрическую формулу Виета.
Разложим многочлен на множители. Y=(x+0,77)*(x-0,88)*(x-5,88)
Нули функции: Х₁ =-0,77, Х₂ =0,88, Х₃ =5,88
(без комментариев, без расчёта).
6. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;-0,77]U[0,88;5,88]
Положительная -Y(x)>0 X∈[-0,77;0,88]U[5,88;+∞)
7. Пересечение с осью OY. Y(0) = 4
8. Исследование на чётность.
В полиноме есть и чётные и нечётные степени - функция общего вида.
Y(-x) ≠ Y(x). Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
9. Первая производная. Y'(x) = 3*x² -12*x = 3*x*(x-4) = 0
Корни Y'(x)=0. Х₄ =0 Х₅=4
Где производная отрицательна (между корнями), там функция убывает.
10. Локальные экстремумы.
Максимум - Ymax(X₄= 0) =4. Минимум - Ymin(X₅ = 4) =-28
11. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;0;]U[4;+∞) , убывает - Х∈[0;4] (между корнями).
ВАЖНО! Функция непрерывная - скобки квадратные.
12. Вторая производная - Y"(x) = 6* x -12 = 6*(х-2) = 0
Корень второй производной - точка перегиба Х₆=2
13. Выпуклая “горка» Х∈(-∞; Х₆ = 2] - производная Y"(x)<0 - отрицательная)
Вогнутая – «ложка» Х∈[Х₆ = 2; +∞).
14. График в приложении. Дополнительно схема/шаблон для анализа функции.

2) 60-4=56
3) 80*8=640
4) 20*5=100
5) 640-100=540
6) 56/8=7
7) 40*7=280
8) 540/6=90
9) 280-90=190
(60-16/4)/8*40-(80*8-20*5)/6=190