Должны были монтировать x мест ежедневно. Тогда закончили бы работы через \frac{1600}x
x
1600
дней. Однако, они стали монтировать по (x+120) мест и завершили работы через \frac{1600}{x+120}
x+120
1600
дней, что на 3 дня меньше, то есть
\begin{gathered}\frac{1600}x-\frac{1600}{x+120}=3\\\frac{1600x+192000-1600x}{x^2+120x}=3\\3x^2+360x=192000\\3x^2+360x-192000=0\;\;\;\div3\\x^2+120x-64000=0\\D=14400+4\cdot64000=270400=520^2\\x_{1,2}=\frac{-120\pm520}{2}\\x_1=200\\x_2=-320\;-\;HE\;nogx.\end{gathered}
x
1600
−
x+120
1600
=3
x
2
+120x
1600x+192000−1600x
=3
3x
2
+360x=192000
3x
2
+360x−192000=0÷3
x
2
+120x−64000=0
D=14400+4⋅64000=270400=520
2
x
1,2
=
2
−120±520
x
1
=200
x
2
=−320−HEnogx.
Изначально должны были монтировать 200 мест ежедневно, монтировали 200+120 = 320 мест.
1. Метод исключения неизвестных.
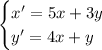
Продифференцируем первое уравнение:
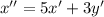
Подставим выражение для y':
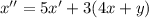
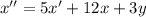
Из получившегося уравнения отнимем первое уравнение системы:
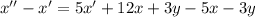
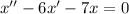
Составим характеристическое уравнение:
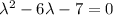
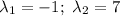
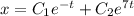
Найдем производную:
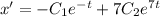
Выразим из первого уравнение системы у:
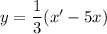
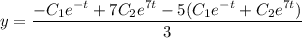
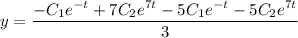
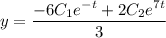
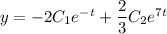
Общее решение:
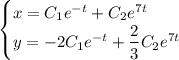
Находим решение задачи Коши:
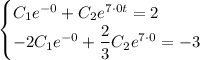
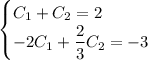
Первое уравнение домножим на 2:
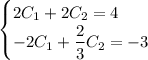
Сложим уравнения:
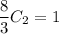
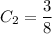
Выразим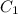 
:
Частное решение:
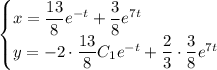
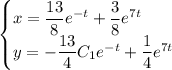
2. Метод характеристических уравнений (метод Эйлера).
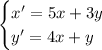
Матрица из коэффициентов при неизвестных:
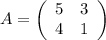
Характеристическая матрица:
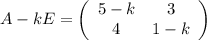
Характеристическое уравнение:
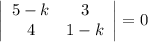
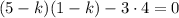
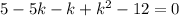
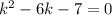
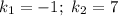
Общее решение:
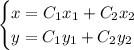
Ищем фундаментальную систему решений:
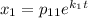
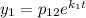
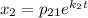
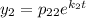
Для нахождения чисел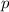 
составим систему:
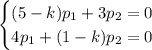
Для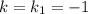 
:
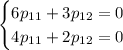
Оба уравнения дают:
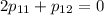
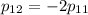
Найдем ненулевое решение. Пусть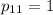 
. Тогда 
.
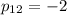Для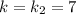 
:
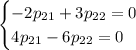
Оба уравнения дают:
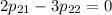
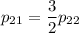
Найдем ненулевое решение. Пусть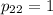 
. Тогда 
.
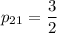Фундаментальная система решений найдена:
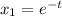
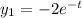
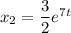
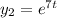
Общее решение:
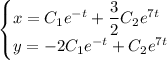
Находим частное решение:
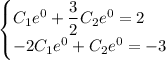
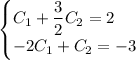
Первое уравнение домножим на 2:
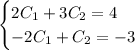
Сложим уравнения:
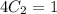
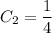
Выразим :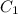
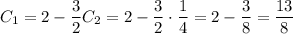
Частное решение:
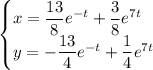
200 : 10 = 20 км/ч - скорость катера
600 : 20 = за 30 часов можно пересечь длину водохранилища
400 : 20 = за 20 часов можно пересечь ширину водохранилища