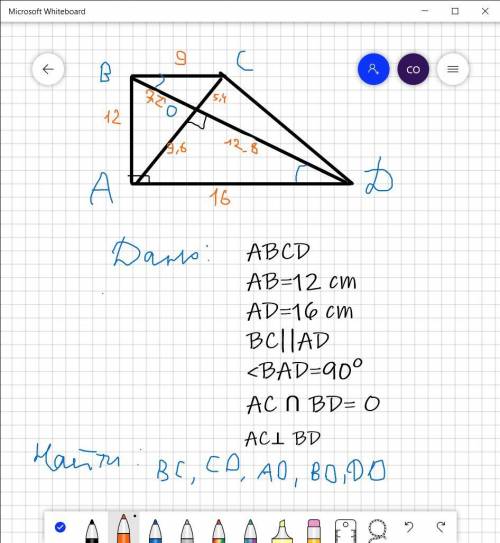
ответ: 9 см; 5,4 см; 9,6 см; 7,2 см; 12,8 см
Пошаговое объяснение:
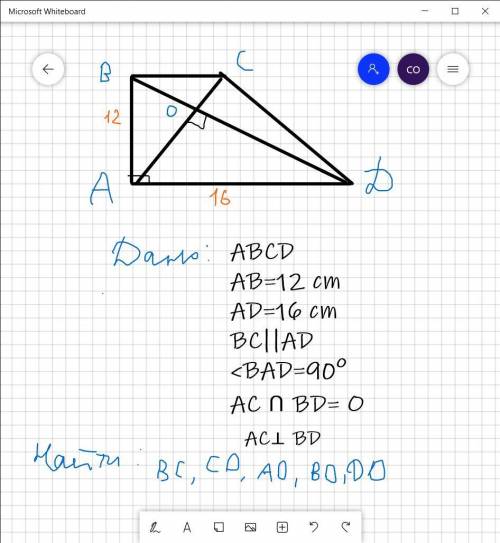
на фото рисунок и дано
Прежде всего мы можем узнать ВД из ΔАВД
Это египетский треугольник, т.к. угол ВАД=90° и катеты соотносятся как 3:4 (12:16=3:4)
k=12/3=4
Поэтому гипотенуза ВД=5k=5*4=20 см
У трегольников ΔАВО и ΔАДО общая сторона--АО. Причем оба прямоугольные, поэтому по теореме Пифагора выводим катет АО из обоих треугольников.
из ΔАВО АО²=АВ²-ОВ²
из ΔАДО АО²=АД²-ОД²
АВ²-ОВ²=АД²-ОД²
И для удобства обозначим ОВ=х, ОД=20-х
12²-х²=16²-(20-х)²
144-х²=256-400+40х-х²
144=256-400+40х
40х=144+400-256
40х=288
х=7,2 см
ОВ=7,2 см
ОД=20-х=20-7,2=12,8 см
Теперь подставляем результат в формулу
АО²=АВ²-ОВ²
АО²=144-(7,2)²=92,16
АО=9,6 см
Т.к. ВС параллельна АД, то ВД--сечная, поэтому их внутренние разносторонние углы СВД и ВДА равны. Также известно, что ВОС=АОД (как вертикальные), из этого делаем вывод, что треугольники ΔДОА ~ΔВОС подобны
Поэтому ВС/АД=ВО/ОД
ВС=АД*ВО/ОД=16*7,2/12,8= 9 см
И, наконец, ОС/АО=ВС/АД
ОС=ОА*ВС/АД=5,4 см
Фотку с обозначеными сторонами тоже оставила
Пусть Сумма всех положительных =Ха, а их число А тогда
Ха/А=4
Тогда Ха=4*А.
Анологично Сумма отрицательных =Хв и их число В
Хв/В=-8
Хв=-8*В
Так как Ха+Хв равна общей сумме всех чисел то
(Ха+Хв)/(А+В)=-3
Заменяем Ха=4*А а Хв=-8*В и решаем
4*А-8*В=-3*А-З*В
7*А=5*В
Общее количество чисел Y=А+В
Тогда А=Y-В подставляем в верхнюю формулу
7*(Y-В)=5*В
7*Y-7*В=5*В
7*Y=12*В
В=7*Y/12
Так как нам известно что общее количество чисел более 40 и менее 48 подставм вместо Y значения его возможные значения от 41 до 47. ответом будет значение Y при катором В будет целочиленным
при Y=41 получаем В=7*41/12≈17,08 не подходит
Y=42 получаем В=7*42/12=17,5 не подходит
Y=43 получаем В=7*43/12≈17,92 не подходит
Y=44 получаем В=7*44/12≈18,33 не подходит
Y=45 получаем В=7*45/12=18,75 не подходит
Y=46 получаем В=7*46/12≈19,17 не подходит
Y=47 получаем В=7*47/12≈19,58 не подходит
Задача не имеет решения.
Но если немного принебречь условием (написано строго меньше 48)
то получим:
при Y=48 получаем В=7*48/12=28 Подходит