Максимально возможная суммарная площадь обзора
Sобщ.=216.6046 ед.²
Пошаговое объяснение:
Поскольку в задании чётко не ограничен минимальный радиус обзора охотников, то примем его за 0 (охотник уснул).
Площадь обзора каждого из охотников представляет собой круг.
Формула площади круга:
S=πR².
Как видно из формулы площади круга, зависимость от радиуса обзора - квадратичная. Это говорит о том, что для получения максимальной площади обзора, лучше получить один максимально большой круг и два оставшихся небольших, чем два одинаковых и один поменьше или три примерно одинаковых круга. Справедливость этого утверждения подтверждает форма графика квадратичной параболы, и понимание того, что при суммировании площадей мы выполняем "линейную" операцию.
Для того, чтобы определить максимальный круг обзора, нам нужно вычислить расстояния между точками, в которых расположены охотники. Для удобства обозначим точки буквами А(4;9), В(5;1); С(12;7).
Найдем АВ: 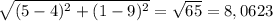
Найдем АС: 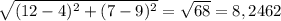
Найдем ВС: 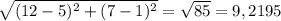
Значит "отдаем приоритет" охотнику в точке С, т.к. два самых длинных расстояния АС и ВС связаны с этой точкой. Охотника в точке А - "усыпляем", т.е. даём ему радиус обзора, равный 0, при этом он вырождается в точку с площадью, равной нулю.
Радиус обзора охотника в точке С принимаем равным АС, иначе если его принять бОльшим, то в площадь обзора включится точка А, что равносильно пересечению участков охотников.
Тогда получаем три площади обзора с радиусами:
0; АС; (ВС-АС)
Вычислим эти площади.
Для точки А: Sa=0 ед.²
Для точки С: Sc=π*АС²=213,6283 ед.²
Для точки В: Sb=π*(BC-АС)²=2.9763 ед.²
Sобщ.=0+213,6283+2,9763=216.6046 ед.²
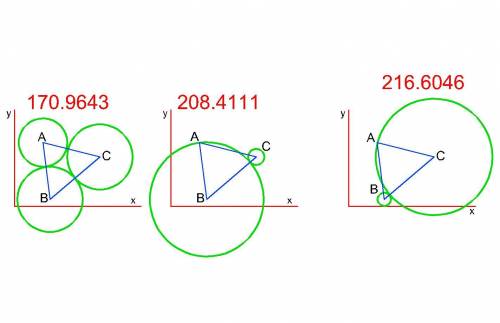
На рисунке прилагаю 3 возможных варианта обзоров охотников из которых только последний (крайний справа) - правильный.
100a+10b+c=11(a+b+c)
89a-b-10c=0
89a=b+10c
очевидно, что это число не больше 200(потому что a=2>89*2=198, которое нельзя представить в виде b+10c(b и с не могут быть меньше 0 и больше 9))
поэтому a=1
89=10c+9
8*10+9=10c+9
отсюда c=8, b=9
поэтому искомое число 198