Для дослідження функції f(x) = x^4 - 12x^2 + 27 спочатку знайдемо її похідні та точки екстремуму.
1. Обчислення похідної:
f'(x) = 4x^3 - 24x
2. Знаходження точок екстремуму:
f'(x) = 0
4x^3 - 24x = 0
4x(x^2 - 6) = 0
Звідси отримуємо дві критичні точки:
x₁ = 0
x₂ = ±√6
3. Визначення значень функції в критичних точках та в кінцях області:
f(x₁) = f(0) = 0^4 - 12(0)^2 + 27 = 27
f(x₂) = f(√6) ≈ -12.73
f(-√6) ≈ -12.73
4. Знаходження інтервалів зростання та спадання:
Знайдемо знаки похідної на різних інтервалах:
-∞ < x < -√6: f'(x) < 0, функція спадає
-√6 < x < 0: f'(x) > 0, функція зростає
0 < x < √6: f'(x) > 0, функція зростає
√6 < x < +∞: f'(x) < 0, функція спадає
5. Виведення результатів та побудова графіку:
- Критичні точки: x₁ = 0, x₂ = ±√6
- Значення функції в критичних точках: f(0) = 27, f(√6) ≈ -12.73, f(-√6) ≈ -12.73
- Інтервали зростання: (-√6, 0) і (0, √6)
- Інтервали спадання: (-∞, -√6) і (√6, +∞)
Графік функції f(x) = x^4 - 12x^2 + 27 буде мати такий вигляд:
^
|
| /
| /
| /
| /
| /
| /
|/
+>
x
Будь ласка, зверніть увагу, що візуалізація графіку краще робиться на графічному інструменті, такому як графічний калькулятор аб
о програма для побудови графіків.
надеюсь правельно понял задание
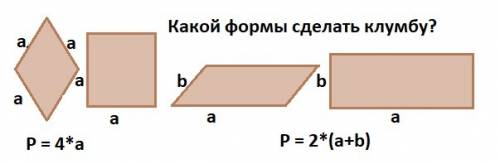
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
6*(1/3у-1)+2*(3-1,5у) = 2y -6 +6 -3y = -y
Упростите и найдите значение выражения при х=2
1,8х-4(0,5х-0,1) = 1,8x-2x+ 0,4 = -0,2x+0,4
-0,2*2+0,4 = -0,4+0,4 = 0