Теорема Безу
Остаток от деления многочлена f(x) на двучлен (x - a) равен f(a)
Доказательство
f(x) = (x - a)·g(x) + r, где g(x) - частное, имеет степень на 1 меньше, чем f(x), а r - число (многочлен степени 0)
Тогда, подставляя x = a получаем:
f(a) = (a - a)·g(a) + r, то есть получаем f(a) = r, или r = f(a) - что и требовалось.
Теорема 2
x = a - корень f(x) ⇔ f(x) делится на (x - a)
Доказательство
из теоремы Безу получаем, что если f(a) = 0 (то есть a - корень f(x)) ⇒ f(x) = (x - a)·g(x) + 0 ⇒ f(x) при делении на (x - a) дает g(x) при 0-м остатке, а значит делится (x - a)
Обратно: раз f(x) делится на (x - a), значит остаток равен 0, а он по теореме Безу равен f(a), то есть a - корень f(x)
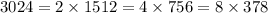- тут мы уже получили 1 возможное число, теперь исследуем число 378.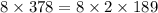
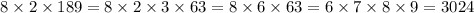, так как 63 = 9*7.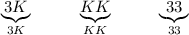
18:3+(2097-96)+54:6+40000=42016
1) 2097-96=2001
2)18/3=6
3)54/6=9
4)6+2001=2007
5)2007+9=2016
6)2016+40000=42016
80000+23*2-(40281-281)-40000=46
1) 40281-281 = 40000
2)23*2=46
3)80000+46=80046
4)80046-40000=40046
5)40046-40000=46
46:2+57:3+17*4+50000=50110
1) 46/2=23
2) 57/3=19
3)17*4=68
4)23+19=42
5)42+68=110
6)110+50000=50110