пусть х-скорость первого автомобиля, а у-скорость второго автомобиля Составим систему из двух уравнений. Первое уравнение 360/у-360/х=0,5 и второе 3х-3у=30 Второе сократим на 3, тогда получим х-у=10. выразим из этого уравнения х=у+10 и подставим в первое уравнение. Получим 360/у-360/(у+10)-0,5=0 Получим 720(у+10)-720у-(у+10)у=0
У^2+10y-7200=0 Найдем через дискриминант корни уравнения D=100+28800=28900=170^2
y₁=80 y₂=-90 (посторонний корень, так как скорость не может быть отрицательной) Следовательно у=80, а х=80+10=90
ответ: скорость первого автомобиля 90 км/ч, а второго 80 км/ч
Пошаговое объяснение
получи решение
Дано: y(x) = 2*x⁵ + 5*x⁴ - 10*x³ + 3
Исследование.
1. Область определения: D(y)= X∈(-∞;+∞).
Гладкая, непрерывная.
2. Вертикальных асимптот - нет.
3. Наклонная асимптота: k = lim(+∞)Y(x0/x = ∞ - асимптот - нет.
4. Нули функции, пересечение с осью ОХ.
Нули функции: х1 = - 3,817, х2 = 0.
Пересечение с осью ОУ: y(0) = 3.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;-3,817].
Положительна: Y>0 - X∈[-3.817;+∞;)
6. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция общего фида.
7. Поиск экстремумов по первой производной.
y'(x) = 10*x⁴+20*x³-30*x² = 10*x²*(x²+2*x+3) =10*x*(x+3)(x-1)= 0.
x1 = -3, x2 = 0, x3 = 1 - точки экстремумов.
8. Локальные экстремумы/
Максимум: y(-3) = 192, минимум: y(0) = 3. y(1) = 0.
9. Интервалы монотонности.
Возрастает - X∈(-∞;-3]∪[1;+∞). Убывает: X∈[-3;0]∪[0;1].
10. Поиск перегибов по второй производной.
y"(x) = 40*x³+ 60*x² - 60*x = 20*x*(2*x²+3*x+3) = 0
x1 = - 2.186, x2 = 0, x3 = 0.686
11. Вогнутая - "ложка"- X∈[-2.186;0],
выпуклая - "горка" - X∈(-∞;-2.186]∪[0;0.686]
12. Область значений. E(y) - y∈(-∞;+∞).
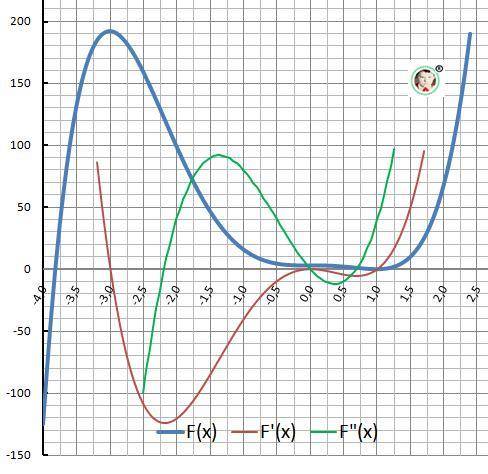
13. График функции на рисунке в приложении.
Волнистыйпопугай — одна из наиболее популярных комнатных птиц, содержащихся у любителей.Его можно встретить повсюду и у самых разных людей — у седовласых профессоров и домохозяек, школьников и вдумчивых исследователей-профессионалов. Многим полюбилась эта птичка, которая и на попугая не очень-то похожа из-за отсутстви яроскошного оперения (правда, есть попугаи, имеющие однотонный окрас, однако их сравнительно немного). Большинство же видов этих птиц имеют яркую, сочную окраску, порой даже «кричащую». Волнистые попугаи стали столь популярны,что «обогнали» в этом отношении даже канареек, долго держащих первенство по количеству птиц в неволе среди декоративных пернатых. Вот чт оговорил про эту птицу биолог Ю.Заблудский: «Волнистый попугайчик необычайно красиво сложен: удлиненное тело, маленькая изящная головка,ступенчатый длинный хвост, удлиненные, остроконечные, как у ласточки,крылья».