5/6 >5/8,_ 17/30< 2/3,_ 79/68 >5/113,_ 11/12 < 19/20,_ 2³/₁₆ < 2⁹/₁₆
Пошаговое объяснение:
1) При сравнении дробей с одинаковым числителем больше та дробь, знаменатель которой меньше.
5/6> 5/8 ( На чем больше частей делится что-то, тем меньше получится каждая часть).
2) 17/30 и 2/3 приведем к общему знаменателю:
17/30 <20/30 ( при сравнении дробей с равными знаменателями больше та, у которой больше числитель. Если что-то разделить на 30 частей , то 17 частей меньше. чем 20 таких же).
3) 79/68 и 5/113
Первое число - неправильная дробь, оно больше едииницы. Второе - меньше единицы. Поэтому
79/68 > 5/113
4) 11/12 и 19/20
Первому числу до целого недостает 1/12, второму 1/20.
Т.к. 1/12> 1/20, то 19/20>11/12 ( см. объяснение п. 1)
5) Из смешанных чисел с равной целой частью больше та, у которого больше дробная часть. 2=2, 9/16>3/16, поэтому 2 целых и 3/16 меньше, чем 2 целых и 9/16.
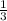 часть всех запасов сахара для дрессуры, то у него осталась
часть всех запасов сахара для дрессуры, то у него осталась 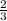 запасов сахара для дрессуры, т.е. в
запасов сахара для дрессуры, т.е. в  раза больше, чем он потратил. Поскольку
раза больше, чем он потратил. Поскольку 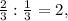 или иначе говоря, поскольку
или иначе говоря, поскольку 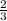 вдвое больше, чем
вдвое больше, чем 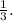
 кусков сахара.
кусков сахара. недели.
недели. недель.
недель.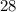 кусков сахара за
кусков сахара за  недели, а значит, в неделю он тратил в два раза меньше, т.е.
недели, а значит, в неделю он тратил в два раза меньше, т.е. 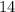 кусков сахара в неделю.
кусков сахара в неделю. кусков сахара в неделю.
кусков сахара в неделю.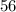 кусков после начальной дрессуры, то при расходе
кусков после начальной дрессуры, то при расходе  кусков сахара в неделю ему хватит этого остаточного запаса на
кусков сахара в неделю ему хватит этого остаточного запаса на 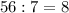 недель.
недель.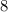 недель.
недель.
1 ур. 26=-3k+b
2 yp. -22=5k+b
Из первого уравнения выразим b
1 ур. 26+3k=b
2 yp. -22=5k+b
Подставим значение первое уравнение во второе и отдельно его решим
-22=5k+26+3k
-22-26=8k
-48=8k
-48/8=k
-6=k
Вернемся в нашу систему
1 ур. 26+3k=b 1 ур. 26+3*(-6)=b 1 ур. 26-18=b 1 ур. 8=b 1 ур. b=8
2 yp. k=-6 2 yp. k=-6 2 yp. k=-6 2 yp. k=-6 2 yp. k=-6
Получили следующую прямую
у=-6x+8
ответ: прямая проходящая через точки A(-3; 26), B(5; -22) записывается в виде у=-6x+8