Найдем сначала общее решение соответствующего однородного дифференциального уравнения
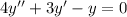
Пусть 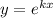 , мы получим характеристическое уравнение
, мы получим характеристическое уравнение
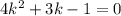
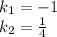
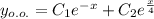 — общее решение однородного диф. ур.
— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию 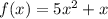
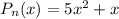 отсюда
отсюда 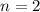 ;
;  . Сравнивая
. Сравнивая 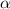 с корнями характеристического уравнения и, принимая во внимая, что
с корнями характеристического уравнения и, принимая во внимая, что  , частное решение будем искать в виде:
, частное решение будем искать в виде:
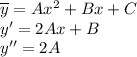
Подставляем в исходное дифференциальное уравнение
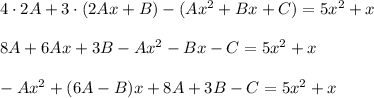
Приравниваем коэффициенты при степени x
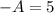 откуда
откуда 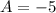
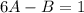 откуда
откуда 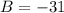
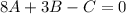 откуда
откуда 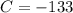
Частное решение: 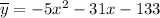
Общее решение линейного неоднородного дифференциального уравнения:
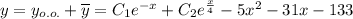
Приведем к общему знаменателю
Применим основное свойство пропорции: произведение крайних членов пропорции равно произведению средних
3·mn=17·(m+n)
Произведение 17(m+n) делится на 17
Значит и произведение слева должно делиться на 17, поэтому либо m, либо n кратно 17
Запишем вместо m выражение 17k, кратное 17 ( k- натуральное)
3·17k·n=17·(17k+n)
3·k·n=17k+n
(3k-1)·n=17k
Либо n, либо 3k-1 кратно 17
3k-1=17p
При k=6
3·6-1=17 - верно
Значит m=17k=17·6=102
ответ. m=102; n=6