13 см
Пошаговое объяснение:
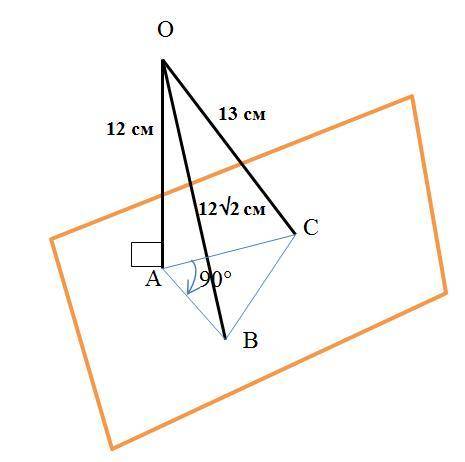
Пусть перпендикуляр, опушенная из точки О пересекает плоскость α в точке А, а наклонные пересекают в точках В и С (см. рисунок). По условию их длины равны: ОА=12 см, ОВ=12√2 см и ОС=13 см.
Так как ОА перпендикуляр, опушенная из точки О к плоскости α, то имеем:
1) проекциями наклонных ОВ и ОС будут АВ и АС;
2) ∠ОАВ=90°, ∠ОАС=90°.
Поэтому по теореме Пифагора, в прямоугольном треугольнике ОАВ: ОВ²=ОА²+АВ², а в прямоугольном треугольнике ОАС: ОС²=ОА²+АС².
Тогда
АВ²=ОВ²-ОА²=(12√2)²-12²=144·2-144=144=12² или АВ=12 см
АС²=ОС²-ОА²=13²-12²=169-144=25= 5² или АС=5 см
Но, по условию, треугольник АВС также прямоугольный. В силу теоремы Пифагора, расстояние между основаниями наклонных находим через катеты АВ и АС:
ВС²=АВ²+АС²=(12 см)² + (5 см)²=144 см² + 25 см² = 169 см²
или ВС= 13 см.
 см i двi похилi, довжини як" />
см i двi похилi, довжини як" />
Здравствуйте!
123
Пошаговое объяснение:
Пусть нахождение этого числа имеет формулу 12×5×x+y, где 1<x<17 (при этом будет выполняться условие трехзначного числа), 0<y<5 (если y<1, то остаток будет нулевым, если y>4, то число будет делится на 5 дополнительно с другим остатком). 12×5- НОК (12;5).
И так, пусть х=2. Тогда число будет:
12×5×2+y=120+y.
Раз 2- среднее арифметическое 1 и y (т.к. при допустимых y мы меняем 3 цифру числа), то:
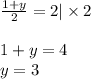
То есть 120+y=120+3=123
Нам требуется привести любое число, которое удовлетворяет условиям.
Проверка:
123÷5=24 (ост. 3)
123÷12=12 (ост. 3)
(1+3)/2=2
С Новым Годом!
2 - 25/60 = 1 35/60 = 1 7/12 = 19/12 - время движение велосипедиста
14 км/ч - скорость движения велосипедиста в гору
14 * 9/7 = 18 км/ч -скорость движения велосипедиста с горы , отсюда имеем
S/14 + S/18 = 19/12 решая уравнения получаем S = 12,5 км расстояние которое проделал велосипедист в гору или с горы