Вектор нормали M₁M₂ = {-10 - (-5); 9 - 5; 6 - 3} = {-5; 4; 3}.
Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали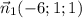 
. Поскольку точки M₁ и М₂ принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
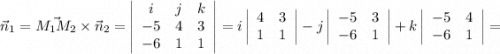
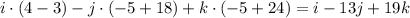
Вектор нормали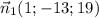 
, т.к. точка 
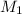принадлежит искомой плоскости, то её координаты должны удовлетворять этой плоскости, т.е. -5 - 13 * 5 + 19 * 3 + D= 0 откуда D = 13.
Итого получаем уравнение плоскости x - 13y + 19z + 13 = 0, где значения B, C, D соответственно равны (-13), 19, 13
96-24,5-66,58=4,92 т осталось на двух складах
4,92:2=2,46 т осталось на каждом складе
2,46+24,5=26,96 т - было на первом складе изначально
2,46+66,58=69,04 т - было на втором складе изначально