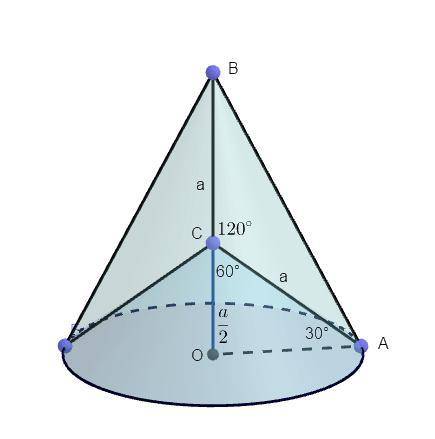
При вращении заданного треугольника вокруг боковой стороны получается тело вращения, состоящее из конуса с образующей AB (основание Δ ABC) и конуса с образующей СА (боковая сторона Δ ABC). Оба конуса имеют равное основание – окружность радиуса OA. Радиус окружности основания конусов – перпендикуляр, опущенный из вершины A ΔABC на ось вращения.
Объем тела вращения (V) будет равен разности объемов большого (V₁) и малого (V₂) конусов. V = V₁ – V₂ ;
Объем конуса V = 1/3 * SoH; So – площадь основания, H – высота конуса.
В прямоугольном треугольнике ΔAOC <ACO = 60⁰ , так как он смежный с заданным углом ΔABC <ACB = 120⁰ (сумма смежных углов = 180⁰). Тогда <OAC = 180⁰ – 90⁰ – 60⁰ = 30⁰. Боковая сторона ΔABC AC является гипотенузой ΔAOC = a. Катет, лежащий против угла 30 равен половине гипотенузы. Высота малого конуса CO = a/2.
Найдем радиус окружности по т.Пифагора из ΔAOC: OA = R; R² = a²– (a/2)² = a² – (a²/4) = 3a²/4; R =a*√3/2;
Площадь основания So=πR² = 3πa²/4;
Высота большого конуса H = a+a/2 = 3a/2;
Объем большого конуса V₁ = 1/3 * 3πa²/4 * 3a/2 = 3πa³/8;
Объем малого конуса V₂ = 1/3 * 3πa²/4 * a/2 = πa³/8;
Объем тела вращения V = V₁ – V₂ = 3πa³/8 - πa³/8 = 2πa³/8 = πa³/4.
Ни одного рыцаря или 2 рыцаря
Пошаговое объяснение:
Решаем перебирая количество рыцарей:
1) Ни одного рыцаря, тогда все 6 жители острова должны быть Лжецами. Так и будет: если каждый из них сказал "Среди остальных пятеро ровно четыре лжеца!", то это Ложь, так как среди остальных пятеро ровно пять лжеца.
2) Только 1 рыцарь, тогда все остальные 5 жители острова должны быть Лжецами. Если рыцарь сказал "Среди остальных пятеро ровно четыре лжеца!", то это Ложь, так как среди остальных пятеро ровно пять лжеца. Это противоречить тому, что рыцари всегда говорят правду!
3) 2 рыцаря, тогда все остальные 4 жители острова должны быть Лжецами. Теперь если один из рыцарей скажет "Среди остальных пятеро ровно четыре лжеца!", то это Истина, потому что другой рыцарь всегда будет с другими 4 лжецами. Если один из лжецов скажет "Среди остальных пятеро ровно четыре лжеца!", то это Ложь, потому что два рыцаря всегда будет с другими 3 лжецами.
4) 3 рыцаря, тогда все остальные 3 жители острова должны быть Лжецами. Теперь если один из рыцарей скажет "Среди остальных пятеро ровно четыре лжеца!", то это Ложь, потому что два рыцаря всегда будет с другими 3 лжецами и количество лжецов не 4 а 3. Это противоречить тому, что рыцари всегда говорят правду!
Если предположит, что количество рыцарей 4, 5 или 6, как в случае 3 рыцарей получаем противоречие с тем, что рыцари всегда говорят правду!
2)3100
3)857.3
4)2094