все в картинках........-----
Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные - машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению - промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.

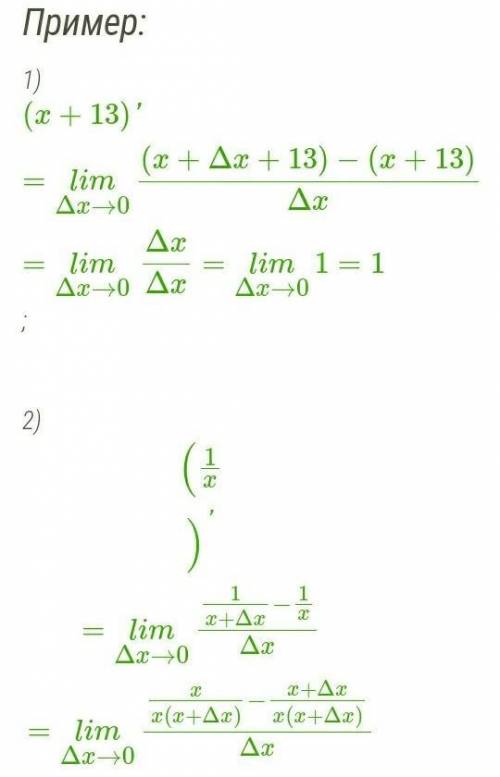

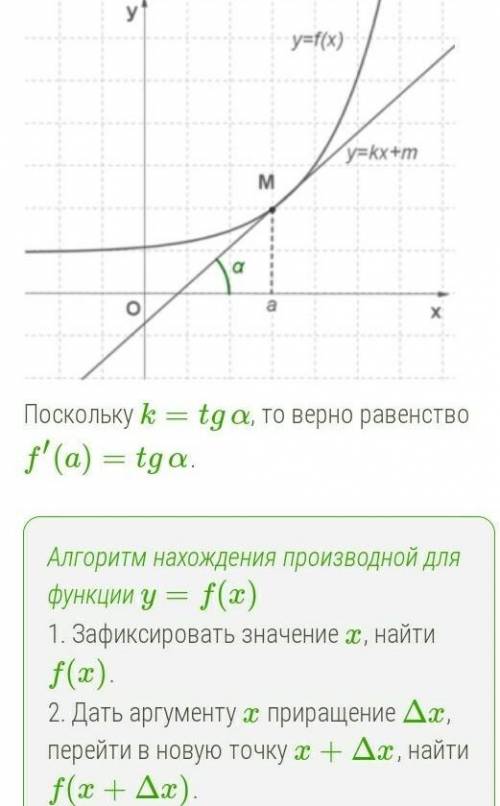

В первом случае cos2x заменяется на sin
Получается 4(1-2sin^2 x)+44sin^2 x - 29=0
4-8 sin^2 x + 44sin^2 x - 29=0
36sin^2 x -25=0
sin^2 x=25/36
sin x= 5/6 sin x= -5/6
Во втором случае cos2x заменяем через косинус
4(2cos^2 x -1) - 10cos x +1=0
8cos^2 x - 4 - 10cos x +1=0
8cos^2 x - 10cos x -3=0
Замена cos x=t t принадлежит (-1;1)
8t^2-10t-3=0
D=100-4*8*(-3)=100+96=196=(14)^2
t=(10+14)/2*8=24/16=1,5 - этот корень не подходит так как больше единицы
t=(10-14)/2*8=(-4)/16=(-0,25)
возвращаемся к подстановке
cos x = -(1/4)
х= +/- arccos (- 1/4 ) + 2Пn
х= +/- (П- arccos (1/4)) + 2Пn
Как-то так =)
тогда во втором (5-х) кг сахара
Составим уравнение:х/3=6(5-х)/7;
7х/21=18(5-х)/21;
7х=18(5-х);
7х=90-18х;
25х=90;
х=3,6(кг)---было в 1-м пакете.
5-х=5-3,6=1,4(кг)---было во 2-м пакете.
ответ:3,6 кг;1,4 кг.