![(2\sqrt2+1)^2-9=8+4\sqrt2+1-9=4\sqrt2=2^2\cdot 2^{0,5}=2^{2,5}\\\\\\2^{log_8{x^{-1}}+2,5}=2^{2,5}\; \; \; \to \; \; \; \; 2^{log_8{x^{-1}}}\cdot 2^{2,5}=2^{2,5}\; ,\\\\2^{log_8{x^{-1}}}=1\; \; \; ,\; \; \; 2^{\frac{1}{3}\, log_2x^{-1}}=1\; \; \; ,\; \; \; 2^{log_2x^{-\frac{1}{3}}}=2^0\; \; ,\; \; \; log_2x^{-\frac{1}{3}}=0\; ,\\\\x^{-\frac{1}{3}}=1\; \; ,\; \; \frac{1}{\sqrt[3]{x}} =1\; \; ,\; \; \; \sqrt[3]{x}=1\; \; ,\; \; x=1\\\\Otvet:\; \; x=1\; .](/tpl/images/0396/8700/76323.png)
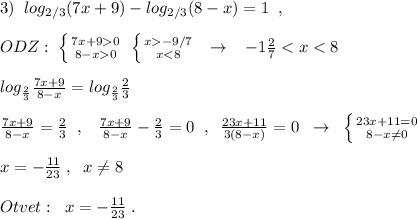
S = a * b
1 сп.
Пусть х см - 1 сторона, тогда 2 сторона будет равна х - 44 см. По условию задачи площадь равна 675см².
Составим уравнение :
675 = х * ( x - 44 )
675 = x² - 44x
x² - 44x - 675 = 0
По теореме, противоположной теореме Виета:
x1 = 22 + √1159
x2 = 22 - √1159
2 сп.
Пусть х см - 2 сторона, тогда 1 сторона будет равна х + 44 см. По условию задачи площадь равна 675 см².
Составим уравнение:
675 = х * ( х + 44 )
675 = х² + 44х
х² + 44х - 675 = 0
По теореме, противоположной теореме Виета:
х1 = -22 + √1159
х2 = -22 - √1159 - корень отрицательный, что не может быть ( сторона не может быть отрицательной ), значит его мы не берём.
ответ: -22 + √1159 см
хорошо.
Пошаговое объяснение:
я тоже прикинь и теперь влюбился в Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.Знакомьтесь с клавиатурой Gboard! Здесь будет сохраняться текст, который вы копируете.Нажмите на фрагмент, чтобы вставить его в текстовое поле.