Неравенство ax² + bx + c < 0 не будет иметь решений, если парабола
y = ax² + bx + c будет расположена над осью Ох или будет касаться оси.
Для этого коэффициент а должен быть положительным, а уравнение ax² + bx + c = 0 не должно иметь корней или иметь один корень, т.е. дискриминант должен быть меньше либо равен нулю:
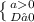
(p - 1) x² + (p - 2) x + 3p - 1 < 0
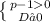
D = (p - 2)² - 4(p - 1)(3p - 1) = p² - 4p + 4 - 12p² + 16p - 4 = - 11p² + 12p
- 11p² + 12p ≤ 0
p(11p - 12) ≥ 0 (см. рис. 1)
p ∈ (- ∞ ; 0] ∪ [12/11 ; + ∞)
p > 1
(см. рис. 2)
p ∈[12/11 ; + ∞)
1. если радиус одной из окружностей равен 4 см, то вторая окружность может быть в 2 раза меньше, а третья- в 2 раза меньше второй:
4:2=2(см)- радиус второй окружности;
2:2=1(см)- радиус третий окружности.
радиус = 1, 2, 4
2. если радиус одной из окружностей равен 4 см, то вторая окружность может быть в 2 раза меньше, а третья- в 2 раза больше:
4:2=2(см)- радиус второй окружности;
4*2=8(см)- радиус третий окружности.
радиус - 2, 4, 8
3. если радиус одной из окружностей равен 4 см, то вторая окружность может быть в 2 раза больше, а третья- в 2 раза больше второй:
4*2=8(см)- радиус второй окружности;
8*2=16(см)-радиус третий окружности.
радиус = 4, 8, 16
81*2/3=54 чел.- получили грамоты
86-5-54=27 детей- ничего не получили
ответ: 27 детей