Решение представлено на фото.
ответ: 2) 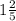
4) 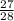
Дана плоскость x-y+2z-2=0 и 2 прямые, заданные параметрическими уравнениями x=1+t, y=2+2t, z=4+3t и x=1-t, y=4+2t, z=-t.
Находим на заданной плоскости точки пересечения с заданными прямыми. Подставим параметрические уравнения прямых в уравнение плоскости:
1 точка: 1 + t - 2 - 2t + 8 + 6t - 2 = 0, 5t = -5, t = -5/5 = -1. (0; 0; 1).
2 точка: 1 - t - 4 - 2t - 2t - 2 = 0, -5t = 5, t = 5/(-5) = -1. (2; 2; 1).
Теперь составляем уравнение прямой, лежащей в заданной плоскости и пересекающей заданные прямые:
(x/2) = (y/2) = (z -1)/0.
2) 17(2-y)/3= 34/10
2-y= 3*2/10
2-y= 3/5
10-5y=3
7=5y
y= 1,4
4) 8,75:5= 19/7-y
1,75=19/7-y
12,25=19-7y
7y=6,75
y= 675/100:7
y= 27/4:7= 27/4*1/7= 27/28