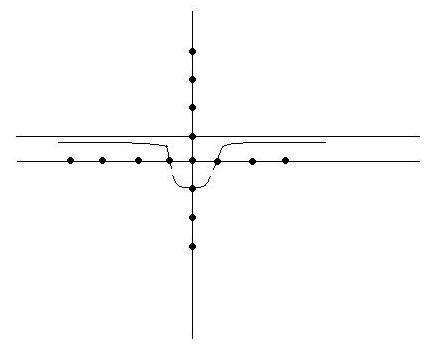
1) ОДЗ: x^2+1#0 - при любом х условие соблюдается. Т.е. функция непрерывная, определена на всей числовой оси.
2) Точки эксремума, промежутки возрастания и убывания ф-ции:
[(x^2-1)/(x^2+1) ]' = (2x*(x^2+1) - (x^2-1)*2x)/(x^2+1)^2 = (2x*( x^2+1-x^2+1))/ (x^2+1)^2=4x/ (x^2+1)^2 = 0, x=0.
x=0 - производная при переходе через эту точку меняет свой знак с минуса на плюс. Значит, это точка минимума. (0; -1) - минимум функции.
При x<0 - функция убывает, при x>0 - возрастает.
3) Нули функции: x=1, x= -1 - в этих точках график функции пересекает ось Ох. (1;0) и (-1;0).
4) В точке y=-1 график функции пересекает ось Оу. (0;-1)
5) Функция четная, симметричная относительно оси Оу.
6) Предел функции при х стремящимся к +бесконечности/-бесконечности равен 1. Значит, график будет приближаться к прямой у=1.
График прикрепляю - очень схематично. Поэтапно отмечаются точки, направления.
Пошаговое объяснение:
1.
а)
1/4х=8
х=8÷1/4
х=8×4/1
х=32
б)
5х-12,5=0
5х=12,5
х=12,5÷5
х=2,5
в)
3х-0,6=х+4,4
3х-х=4,4+0,6
2х=5
х=5÷2
х=2,5
г)
4х-(7х-2)=17
4х-7х+2=17
-3х=17-2
-3х=15
х=15÷(-3)
х=-5
2.
АС=60
АВ:ВС=4:1
4+1=5 частей составляет весь отрезок АС
60÷5=12см приходится на одну часть
12×1=12см отрезок ВС
3.
Пусть во втором контейнере х кг моркови,
Тогда в первом 5х кг моркови
5х-25=15+х
5х-х=15+25
4х=40
х=40÷4
х=10,
Значит во втором контейнере было 10кг моркови,
А в первом 5×10=50кг моркови
4.
3х-(9х-3)=3×(4-2х)
3х-9х+3=12-6х
-6х+6х=12-3
0=9
Уравнение не имеет решений