ответ:....
Пошаговое объяснение:
номер 327.
1 уравнение.
x(3x +2) - 5(3x + 2)=0
3x^2 + 2x -15x -10 =0
3x^2 +13x -10=0
Решение дискриминантом.
Дискриминант D квадратного трёхчлена ax2 + bx + c равен b2 - 4ac.
b, a, c - это коэффициенты. a=3, b=13, c=-10
Корни квадратного уравнения зависят от знака дискриминанта (D) :
D > 0 - уравнение имеет 2 различных вещественных корня;
D = 0 - уравнение имеет 1 корень (или же 2 совпадающих вещественных корня)
D=(13)^2-4*3*(-10)=169+120=289
корень из дискриминанта равен 17.
Находим корни по формуле.(фото)
x1=-13+17/2*3=4/6=2/3
x2= -13 -17 /2*3=-30/6=-5
По такому принципу решаем все уравнения.
1)число перед скобкой умножается на всю скобку
2)внимательней со знаками.Минус на минус=плюс
минус на плюс=минус
3)x*x=x^2(x в квадрате)
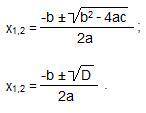
№1
Примем
А - количество одногривенных
В - количество двугривенных
1 грив=0,1 руб
2 грив=0,2 руб
тогда
0,1*А+0,2*В=27
А+В=170
А=170-Б
0,1*(170-В)+0,2*В=27
17-0,1*В+0,2*В=27
0,1*В=10
В=100 - количество двугривенных
А=170-100=70 - количество одногривенных
2)
Примем
х - количество учеников Пифагора
тогда
х-х*1/2-х*1/4-х*1/7=3
х*28/28-х*14/28-х*7/28-х*4/28=3*28/28
х*(28-14-7-4)/28=3*28/28
х*3/28=3*28/28
х=(3*28/28)/(3/28)=28 - количество учеников Пифагора
3)
примем
а-количество жетонов в первом мешке
в-количество жетонов во втором мешке
тогда
а+в=250
а-25=в+25
а=в+25+25=в+50
в+50+в=250
2*в=200
в=200/2=100-количество жетонов во втором мешке
тогда
а=100+50=150-количество жетонов в первом мешке
466-х=103
х=466-103
х=363
(466-363)=*12=1236
1236=1236
ответ:х=363