5; 10; 15; 20; ....
Рассмотрим эту арифметическую прогрессию с первым членом а₁=5 и разностью d=5
n - число натуральных чисел
ОДЗ: n ∈ N
Сумма S первых членов арифметической прогрессии вычисляется по формуле:
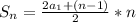
в нашем случае
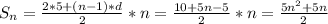
По условию
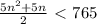
Найдем наибольшее натуральное решение этого неравенства . Для этого найдём корни уравнения:
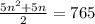
5n² + 5n = 765*2
5n² + 5n - 1530 = 0
n² + n - 306 = 0
D = b² - 4ac
D = 1² - 4 * 1 * (-306) = 1225
√D = √1225 = 35
n₁ = (-1 - 35)/2 = - 18 отрицательное значение не удовл. ОДЗ
n₂ = (-1 + 35)/2 = 17 - удовлетворяет ОДЗ
При n=17 сумма 17 слагаемых равна 765.
Следовательно, наибольшее натуральное число, для которого сумма будет меньше 765, равно 16.
n<17 => n=16
ответ: n=16
2 склад: 2,5*x
x+180= 2,5*x + 60
120 = 1,5x
x=80 - на первом складе
2,5x=2,5x*80 = 200 - на втором складе