1. длины сторон треугольника относятся как 4: 5: 7. найдите периметр треугольника, если сумма его наибольшей и наименьшей сторон равна 44 см. 2) вычеслить 6: 1целая3/8-39,6+1целая3/7

👇

Ответ:

egorovaesya

27.09.2022

Наибольший угол лежит против большей стороны, наименьший - против наименьшей стороны.то стороны 1и 3 в пропорции.

составим сумму частей 4+7=11 - одна часть суммы сторон 11: всего 44 см⇒
1часть 44/11=4 см. Большая сторона 7*4=28 см, меньшая 4*4=16 см
проверим: 16+28=44 и 16/28=4/7.

Найдем среднюю по величине сторону. Обозначим ее х. 16/х=4/5
отсюда х=16*5/4=4*5=20 см. периметр Р=16+20+28=64

4,8(23 оценок)

Ответ:

ElizavetaMusic

27.09.2022

Пусть к - коэффициент пропорциональности. Тогда 4к + 7к = 44

к = 4. Значит, стороны треугольника 16 см, 20 см, 28 см, а периметр 16+20+28=64 см.

4,5(22 оценок)

Открыть все ответы

Ответ:

sahabg

27.09.2022

А) Длины экваторов - это другими словами длина окружности с радиусом, равным половине данного диаметра.

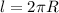$l=2 \pi R$ длина окружности
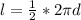
$l= \frac{1}{2}* 2 \pi d$
$l= \pi d$
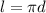
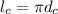$l_{c} = \pi d_{c}$ длина экватора Сатурна
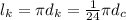$l_{k} = \pi d_{k}= \frac{1}{24} \pi d_{c}$ длина экватора Каллисто
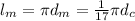$l_{m} = \pi d_{m}= \frac{1}{17} \pi d_{c}$ длина экватора Марса

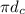Во всех трех формулах $\pi d_{c}$ одинаково, значит можно рассматривать только коэффициенты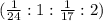

$( \frac{1}{24} : 1 : \frac{1}{17} :2)$

В итоге отношения экваторов планет и диаметров планет получились похожи.

б)Во сколько раз больше... Это значит, что диаметр Марса нужно поделить на диаметр Каллисто

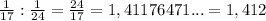
$\frac{1}{17} : \frac{1}{24} = \frac{24}{17} =1,41176471...=1,412$

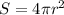в) $S=4 \pi r^{2}$ - площадь поверхности шара

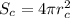$S_{c} = 4 \pi r_{c} ^{2}$ площадь поверхности Сатурна
$S_{k} = 4 \pi r_{k} ^{2}=4* \frac{1}{ 24^{2} } \pi r_{c} ^{2}=\frac{4}{ 576 } \pi r_{c} ^{2}$ площадь поверхности Каллисто
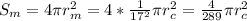$S_{m} = 4 \pi r_{m} ^{2}=4* \frac{1}{ 17^{2} } \pi r_{c} ^{2}=\frac{4}{ 289 } \pi r_{c} ^{2}$ площадь поверхности Марса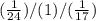

Из данных Уравнений мы видим,что площади соотносятся как
4/576 : 4 : 4/289. Поделим эти значения на 4 и получим
1/576 : 1 : 1/289.

ответ: а) $( \frac{1}{24})/(1)/( \frac{1}{17})$
б)1,412
в)1/576 : 1 : 1/289

Комментарий.
Если заметили, то отношения экваторов и радиусов получились похожими, т.е. их можно и не вычислять.
Длина окружности и радиус - величины в первой степени.

Отношения площадей - это отношения радиусов/диаметров в квадрате, т.к. площадь - величина второй степени (в квадрате)

4,7(72 оценок)

Ответ:

L1mbada

27.09.2022

Предположим, что у нас ровно k коробок полные. Тогда ровно k утверждений верно.
Утверждение: "хотя бы n коробок пустые" можно перефразировать как "максимум 2014-n коробок полные"
Тогда при k полных коробках можно определить истинность надписей на коробках.
1) 2014 коробок пустые - 0 коробок полные - не верно
2) хотя бы 2013 коробок пустые - максимум 1 полная - не верно
...
k) хотя бы 2015-k пустые - максимум k-1 полных - не верно
k+1) хотя бы 2014-k пустые - максимум k полных - верно
k+2) хотя бы 2013-k пустые - максимум k+1 полных - верно
...
2014) хотя бы 1 пустая - максимум 2013 полных - верно
Видно, что пункты с 1 по k-й не верны, а пункты с k+1 по 2014 верные. Количество верных пунктов: 2014 - (k+1) + 1 = 2014-k. Оно равно, как мы условились, количеству полных коробок. То есть 2014-k=k. Отсюда k=1007.

4,7(96 оценок)

Это интересно:

Компьютеры-и-электроника

11.10.2020

Как снять летсплей или как делать профессиональные видеоинструкции для YouTube?...

Дом-и-сад

13.12.2020

Простые способы удаления жевательной резинки с бетона...

Финансы-и-бизнес

14.01.2023

Рассчитываем налог на собственность: полезные советы и всё, что нужно знать...

Компьютеры-и-электроника