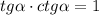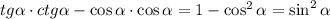
18 - 9 - 9 -(2 - 3 - (1/3)) = 1 1/3 = 4/3 ≈ 1.3333. 
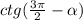— здесь 
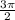, значит меняем на 
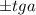; Выясним знак: 
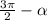— это III (3-я) четверть, значит тангенс с плюсом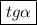 
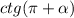— здесь 
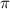, значит оставляем 
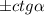. Выясним знак: 
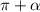— это III (3-я) четверть, значит котангенс с плюсом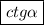 
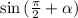— здесь 
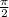, значит меняем на 
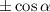. Выясним знак: 
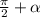— это II (2-я) четверть — синус имеет знак +, значит косинус тоже 
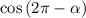— здесь 
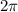, значит оставляем 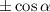. Выясним знак: 
— это IV (4-я) четверть, значит косинус с плюсом 
