Пошаговое объяснение:
чтобы найти уравнение траектории точки, надо из обоих уравнений исключить параметр t
x=4t² (умножим на 3)
y=2+3t² (умножим на -4)
и сложим уравнения
3x = 12t²
-4y =-8 -12t²
3x -4y +8 = 0 - это уравнение траектории. построим эту прямую в координатах оху (строим по двум точкам x=0, y = 2; x=4, y = 5)
теперь скорость
проекции скорости на ох и оу
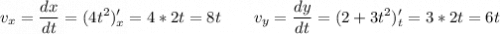
тогда модуль скорости
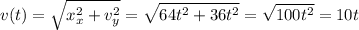
и скорость в момент времени t = 1.5c
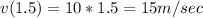
теперь ускорение
проекции ускорения на оси ох и оу

тогда ускорение
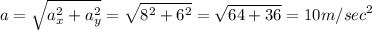
итак, ответ
рівняння траєкторії точки 3x -4y +8 = 0
її швидкість в момент часу 1,5 с v= 15 м/c
її прискорення в момент часу 1,5 с а = 10 м/с²
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков. Будем считать задачу «красной» , если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков) . Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику. Тогда каждая клетка соответствует паре «мальчик–девочка» . Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец. По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 • 10 + 21 • 10 < 21²).
Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток. Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками. Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой. В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.
Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.
2)8*3= 24
3)88+24=112