Відповідь:
Покрокове пояснення:
1) d = r + 8
d = 2r
2r = r + 8
r = 8
l = 2πr = 16π ≈50,24 см
2) l = 2πr
r = l / 2π
r1 = 2/2π = 1/π ≈ 0,32 см
r2 = 5/2π = 2,5/π≈0,8 см
r3 = 3,14/π ≈ 1 см
r4 = 4 * 
/π≈4 * 3,14 = 12,56 см
3) l1 = 2πr * 1 / 360 = πr/180 ≈ 0,1 см
l2= 2πr * 15/360 = 2πr/24 = πr/12 ≈1,57 см
l3 = 2πr * 120/360 = 2πr/3 ≈12,56 см
l4 = 2πr * 270/360 = πr * 3 / 2 ≈28,26 см
l5 = 2πr * 330/360 = πr * 11 / 6 = 34,54 см
4) l = 2πr * 18 / 360 = πr/10 = 15
r = 150/π ≈ 47,8°
5) l = 2πr * α / 360 = πr * α / 180
α = 180 * l / πr ≈ 12 см
а) 6х – 11,4 = 3,48
Перенесем известные величины в правую часть уравнения.
6х=3,48+11,4
Приводим подобные члены.
6х=14,88
Разделим левую и правую часть уравнения на коэффициент при неизвестном.
х=14,88:6
x=2.48
б) 3х + 5х + 0,26 = 6,7
Приводим подобные члены.
8х+0,26=6,7
Перенесем известные величины в правую часть уравнения.
8х=6,7-0,26
Приводим подобные члены.
8х=6,44
Разделим левую и правую часть уравнения на коэффициент при неизвестном.
х=6,44:8
x=0.805
в) (х + 7,2) ⋅ 4,2 = 30,996
х+7,2=30,996:4,2
x+7.2=7.38
Перенесем известные величины в правую часть уравнения.
х=7, 38-7,2
Приводим подобные члены.
х=0,18
г) 216 : х – 9,3 = 50,7
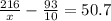
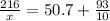
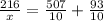
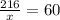
216=60x
60x=216
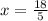
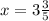или x=3.6
