Пусть - это та часть поля, которую вспахивает 1-ый тракторист за 1 день, а - та часть поля, которую вспахивает уже 2-ой тракторист, но тоже за 1 день.
Мы можем составить систему уравнений!
За 4 дня первый тракторист вспашет части поля, а второй - части поля. И, по условию, сумма этих двух чисел равна 1 (полю).
Время, за которое 1-ый трактор вспашет поля составляет , а то время, за которое второй трактор вспашет поля равно не иначе, как . И сумма этих двух отрезков времени - 10 дней.
Есть две переменных - но и есть два уравнения:
Можем сделать подстановку:
Дальше, воспользовавшись формулой корней полного квадратного уравнения , получим:
Осталось только -и найти:
Итак, у нас есть два решения, и между ними придется сделать выбор.
По условию дано, что " ... первый работает медленнее ... ". Это означает, что .
Но под этот критерий подходит только первое решение (так как ):
Если мы сделаем проверку, то это решение будет удовлетворять всем условиям.
Но все же заметим, что пока ответа задачи у нас нет. Так что самое время его получить.
(дней)
(дней)
Задача [наконец] решена!
первый тракторист может вспахать поле за дней,
а второй - за дней.
- это та часть поля, которую вспахивает 1-ый тракторист за 1 день, а 
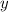- та часть поля, которую вспахивает уже 2-ой тракторист, но тоже за 1 день.Мы можем составить систему уравнений!
За 4 дня первый тракторист вспашет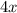
части поля, а второй - 
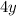части поля. И, по условию, сумма этих двух чисел равна 1 (полю).Время, за которое 1-ый трактор вспашет 
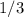поля составляет 
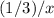, а то время, за которое второй трактор вспашет 
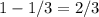поля равно не иначе, как 
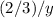. И сумма этих двух отрезков времени - 10 дней.Есть две переменных - но и есть два уравнения:
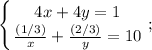
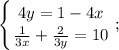
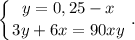
Можем сделать подстановку:
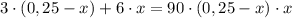
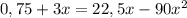
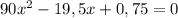
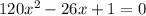
Дальше, воспользовавшись формулой корней полного квадратного уравнения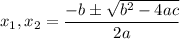 
, получим:
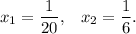
Осталось только 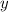-и найти:
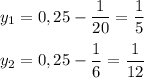
Итак, у нас есть два решения, и между ними придется сделать выбор.
По условию дано, что " ... первый работает медленнее ... ". Это означает, что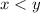 
.
Но под этот критерий подходит только первое решение (так как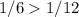 
):
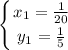
Если мы сделаем проверку, то это решение будет удовлетворять всем условиям.
Но все же заметим, что пока ответа задачи у нас нет. Так что самое время его получить.
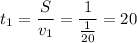(дней)
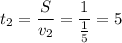(дней)
Задача [наконец] решена!
ответ:первый тракторист может вспахать поле за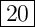 
дней,
а второй - за 
дней.
{ -x > 0
{ x+6 > 0
{ x < 0
{ x > -6
-6 < x < 0
Решаем уравнение
2log3 (-x) = 1 + log3 (x+6)
log3 (-x)^2 = log3 (3) + log3 (x+6) = log3 (3(x+6))
Основания логарифмов одинаковые, переходим к числам под логарифмами
x^2 = 3(x+6)
x^2 - 3x - 18 = 0
(x - 6)(x + 3) = 0
x = 6 - не подходит под область определения
x = -3
2) Область определения
x^2 - 2x > 0
x(x - 2) > 0
x < 0 U x > 2
Решаем уравнение
log2 (x^2 - 2x) = 3
x^2 - 2x = 2^3 = 8
x^2 - 2x - 8 = 0
(x + 2)(x - 4) = 0
x1 = -2, x2 = 4
Оба корня подходят под область определения.