- числитель исходной дроби, тогда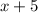 
- знаменатель этой же дроби. 
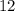получилась дробь, которая в 
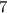раз больше исходной. Так как знаменатель остался прежним, то числитель второй дроби в 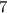раз больше числителя исходной дроби.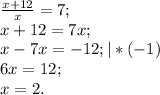
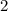- числитель исходной дроби.
.
.
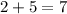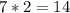А) 3а< 3·5,4
3a < 16,2
б) 3а-5< 16,2- 5
3a-5 <11,2
В) -2а+1
-2a > -2·5,4
- 2a > -10, 8
-2a + 1 > - 10,8 + 1
-2a + 1 > - 9, 8
Г) 1/а+2
1/a - ответить на вопрос нельзя. неизвестно а >0 или а < 0
правило: если a> b > 0, то 1/a < 1/b
10> 5
1/10 < 1/5
Поэтому
если 0<a< 5,4 , то 1/а > 1/5,4=5/27
(1/а) +2 > 2 целых 5/27
или
если в условии речь идет о выражении (а+2) в знаменателе, то решение такое:
если 0<a< 5,4 ,
2< a+2<7,4
то 1/(а+2) > 1/7,4=5/37