Пусть a, b, c - первые три члена арифметической прогрессии, тогда по условию:
а + b + с = 15 [1]
По свойству арифметической прогрессии:
b - а = с - b
2b = а + с подставим в уравнение [1], получим:
2b + b = 15
3b = 15
b = 5 - второй член арифметической прогрессии.
Тогда сумма первого и третьего членов:
а + с = 15 - 5
а + с = 10 ⇒ c = 10 - a
Переходим к геометрической прогрессии. По условию:
первый член = а + 1
второй член = b + 3 = 5 + 3 = 8
третий член = с + 9 = 10 - a + 9 = 19 - a
По свойству геометрической прогрессии:
не удовл.условию, так как искомая геометрическая прогрессия возрастающая.
Получили а = 3, тогда с = 10 - а = 10 - 3 = 7
Итак, первые три члена арифметической прогрессии: 3; 5; 7.
Найдем три первых члена геометрической прогрессии:
первый член = а + 1 = 3 + 1 = 4
второй член = 8
третий член = с + 9 = 7 + 9 = 16
Искомая геометрическая прогрессия: 4; 8; 16; ...
Найдем сумму 7 первых членов.
b₁ = 4 - первый член
q = b₂/b₁ = 8/4 = 2 - знаменатель прогрессии
Искомая сумма:
ответ: 508
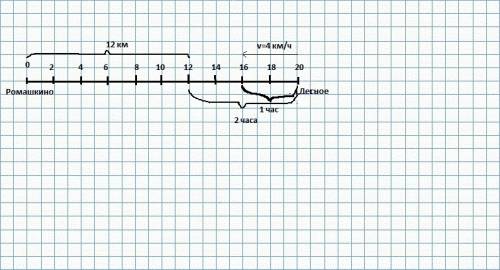
1. Построим шкалу с ценой деления 2 км. Поскольку расстояние между Ромашкино и Лесное равно 20 км, 20÷2=10 делений по 2 км. 1 деление = 1 см, всего нужно сделать 10 делений.
2. Известно, что S (расстояние)=v(скорость)*t(время). Нам нужно узнать время, т.е. t. t=s÷v
В задаче нам дано, что скорость пешехода v=4 км в час.
Определим величину S. Поскольку пешеход вышел из Лесного в Ромашкино, и до Ромашкино ему осталось пройти 12 км, значит он км.
S=8 км.
t=8÷4=2 (часа)
ответ: Пешеход находился на расстоянии 12 км от Ромашкино через 2 часа после выхода из Лесного.
