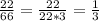
Обозначим скорость работы первой бригады как «х», а скорость работы второй бригады — как «у».
Работая вместе, их общая ставка составляет 1/20 (поскольку они могут проложить весь участок дороги за 20 дней).
Если первая бригада проложит часть участка дороги, а затем ее заменят 6 других, то весь участок дороги будет заасфальтирован за 35 дней. Обозначим количество участков дороги, проложенных первой бригадой, как «а».
Затем второй бригаде нужно будет проложить (1-а) участок дороги.
Работа, которую выполняет первая бригада на участке пути «а», выражается формулой: (а/х).
Затем 6 других рабочих будут заменять эту часть дороги за то же время. Таким образом, мы можем представить их скорость работы как (a/6x).
Работа, которую выполняет второй экипаж, представлена формулой: ((1-а)/у).
Поскольку все они работают вместе, их общая скорость работы составляет 1/35.
Собрав все вместе, мы получим следующее уравнение:
(а/х) + (а/6х) + ((1-а)/у) = 1/35
Упрощая, получаем:
7а/6х + (1-а)/у = 1/35
Мы также знаем, что их общая скорость работы, когда они работают вместе, составляет 1/20, поэтому:
х + у = 20
Теперь у нас есть два уравнения:
7а/6х + (1-а)/у = 1/35
х + у = 20
Находя «а» во втором уравнении, получаем:
а = 20 - у
Подставляя это в первое уравнение, получаем:
7(20-у)/6х + (1-(20-у))/у = 1/35
Упрощение:
(7/6х - 1/у)у + 1/у = 1/35
Умножение обеих сторон на 6xy:
7у - 6х = (6ху)/35
Умножение обеих сторон на 35:
245у - 210х = 6ху
Теперь у нас есть два уравнения:
х + у = 20
245у - 210х = 6ху
Мы можем изменить первое уравнение, чтобы найти «x»:
х = 20 - у
Подставляя это во второе уравнение, получаем:
245 лет - 210 (20 лет) = 6 лет (20 лет)
Упрощение:
245 лет - 4200 + 210 лет = 120 лет - 6 лет ^ 2
Упрощая дальше:
6г^2 - 335г + 4200 = 0
Мы можем найти «y», используя квадратичную формулу:
y = (335 ± sqrt (335 ^ 2 - 4 (6) (4200))) / (2 (6))
у = 15 или у = 50/3
Если у = 15, то х = 5.
Если y = 50/3, то x = 50/3 - 20 = -10/3, что не имеет смысла.
Следовательно, первая бригада может проложить весь участок дороги за 5 дней, а вторая бригада — за 15 дней.
Відповідь:
Покрокове пояснення:
Позначимо ширину прямокутника як x (в см). За умовою, довжина прямокутника дорівнює x + 14,6 (в см).
Периметр прямокутника можна обчислити за формулою:
Периметр = 2 * (довжина + ширина)
Замінюємо дані в формулі:
68,8 = 2 * (x + (x + 14,6))
Розкриваємо дужки та спрощуємо вираз:
68,8 = 2 * (2x + 14,6)
68,8 = 4x + 29,2
Переносимо 29,2 на іншу сторону рівності:
68,8 - 29,2 = 4x
39,6 = 4x
Ділимо обидві частини на 4:
9,9 = x
Отримали, що ширина прямокутника x = 9,9 см.
Довжина прямокутника дорівнює x + 14,6 = 9,9 + 14,6 = 24,5 см.
Площа прямокутника обчислюється за формулою:
Площа = довжина * ширина
Підставляємо значення:
Площа = 24,5 * 9,9
Площа = 241,95 см²
Таким чином, площа прямокутника становить 241,95 квадратних сантиметрів.
22/66 = 2/6 = 1/3