Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была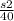 
, а после встречи 
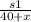. Скорость второго пешехода до встречи и после встречи была одинаковой, значит 
, откуда 
. У первого пешехода до встречи была скорость 
, а после встречи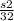 
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 
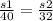, откуда 
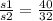. По условию задачи составим уравнение
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 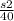, а после встречи 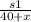. Скорость второго пешехода до встречи и после встречи была одинаковой, значит , откуда . У первого пешехода до встречи была скорость , а после встречи 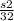, скорость первого пешехода до встречи и после встречи была одинаковой, значит 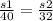, откуда 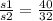. По условию задачи составим уравнение.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
Боковые грани - равносторонние треугольники со сторонами по 1.
Апофема равна 1*cos 30 = √3/2.
Полученный в сечении треугольник - равнобедренный, с боковыми сторонами (апофемами) по √3/2 и основанием, равным 1(стороне квадрата в основании пирамиды). Плоскость этого треугольника перпендикулярна заданным граням, поэтому угол в вершине его - это искомый угол.
По трём сторонам треугольника находим углы по формуле:
cos B = (a²+c²-b²)/2ac.
a b c p 2p S 2 0.866025 1 0.8660254 1.3660254 2.732050808 0.35355339 0.75 1 0.75 1 cos A = 0.5773503 cos B = 0.3333333 cos С = 0.57735027 пи Аrad = 0.9553166 Brad = 1.2309594 Сrad = 0.95531662 3.141593 3.141593 Аgr = 54.73561 Bgr = 70.528779 Сgr = 54.7356103 180 - сумма углов.
cos B = ((3/4)+(3/4)-1)/(2*(√3/2)*(√3/2)) = 1/3 ≈ 0,33333.