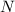деталей, с первого за это же время успевает выйти в два раза больше деталей, т.е. 
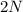. А всего с двух конвейеров выходит 
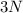деталей. Тогда удобно рассмотреть период времени, когда выпускается некоторое большое число деталей, кратное трём. Возьмём для дальнейших рассуждений такой период, за который выпускается 
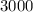деталей.
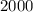деталей и из них 
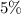, т.е. 
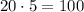бракованных.
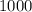деталей и из них 
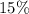, т.е. 
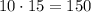бракованных. 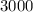деталей брак случился при изготовлении 
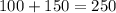деталей.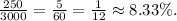
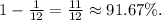
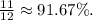
{10-x²-3x≥0
1-x≥0
1-x≠0
⇒{-x²-3x+10≥0 {-(x-2)*(x+5)≥0 {(x-2)*(x+5)≤0
1-x>0 -x>-1 x<1
\ \ \ \ \ \ \ \ \ \ \ \
|||>x
-5 1 2
/ / / / / / / / / / / /
x∈[-5;1)