Комбинаторная задача.
Формула число сочитаний n по к
C = n! / k!(n-k)!
n = 5 всегда
Группа содержит 1 машину (k=1), остальные в другой,
подставляем в формулу
С = 5!/1!*(5-1)! = 5
Группа содержит 2 машины (k=2), остальные в другой,
подставляем в формулу
С = 5!/2!*(5-2)! = 10
ну дальше не буду рассписывать, считаем С для 3 машины
С=5!/ 3! * 2!=10
считаем С для 4 машин
С=5!/ 4! * 1!=5
считаем С для 5 машин
С=5!/ 5! * 0!=1
считаем С для 0 машин
С=5!/ 0! * 5!=1
суммируем все С = 5+10+10+5+1+1 = 32
Держи спрашивала у учёного.
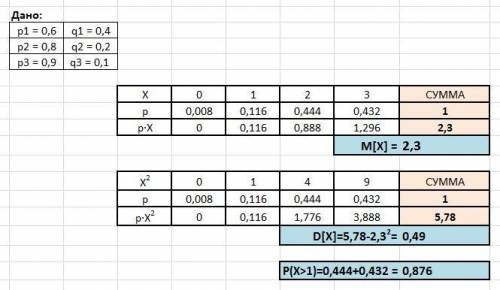
Решим задачу в Excel (см. приложение)
Необходимые пояснения:
Вероятность покупки (и не покупки):
p₁ = 0,6; q₁ = 1 - p₁ = 0,4
p₂ = 0,8; q₂ = 1 - p₂ = 0,2
p₃ = 0,9; q₂ = 1 - p₃ = 0,1.
Ряд распределения.
Число покупок:
X₀ = 0 - покупок не сделано;
X₁ = 1 - покупка сделана только одним покупателем;
X₂ = 2 - покупку сделали двое покупателей;
X₃ = 3 - покупку сделали все покупатели.
Функция распределения.
Всевозможные исходы:
P₀ = q₁·q₂·q₃ = 0,008;
P₁ = p₁·q₂·q₃ + q₁·p₂·q₃ + q₁·q₂·p₃ = 0,116;
P₂ = p₁·p₂·q₃ + p₁·q₂·p₃ + q₁·q₂·p₃ = 0,444;
P₃ = p₁·p₂·p₃ = 0,432.
Проверка:
0,008+0,116+0,444+0,432 = 1
Математическое ожидание:
M[X] = 0·0,008 + 1·0,116 + 2·0,444 + 3·0,432 = 2,3
Дисперсия:
D[X] = 0²·0,008 + 1²·0,116 + 2²·0,444 + 3²·0,432 - 2,3² = 0,49
Вероятность
P(x>1) = 0,444+0,432=0,876
5×0,5=2,5 кг
200/2,5=80 центов стоит 1 кг
ответ: 1 кг