Пошаговое объяснение:
Пусть х - общее количество стульев.
Савелий - 1/2х + 2
х - (1/2х + 2) = х - 1/2х - 2 = (1/2х - 2) - оставшиеся стулья
Игорь - 1/2 · (1/2х - 2) + 2 = 1/4х - 1 + 2 = 1/4х + 1
Арсений - 10 стульев
Уравнение:
х = 1/2х + 2 + 1/4х + 1 + 10
х - 1/2х - 1/4х = 2 + 1 + 10
х - (2/4х + 1/4х) = 13
х - 3/4х = 13
1/4х = 13
х = 13 : 1/4
х = 13 · 4/1
х = 52
ответ: всего 52 стула мальчики принесли в библиотеку.
Проверка:
Савелий - 52 : 2 + 2 = 26 + 2 = 28 стульев
52 - 28 = 24 - оставшиеся стулья
Игорь 24 : 2 + 2 = 12 + 2 = 14 стульев
28 + 14 + 10 = 52 - всего стульев
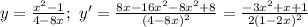
Найдём сумму первых семи членов арифметической прогрессии
S = (2a₁ + (n-1)d) * n /2
S₇ = (2a₁ + 6d) * 7 / 2 = (a₁ + 3d) * 7
По условию эта сумма равна 30.
S₇ = 30
(a₁ + 3d) * 7 = 30 => 7a₁ + 21d = 30
2.
Найдём сумму трёх следующих членов арифметической прогрессии (с 8 по 10)
S₈₋₁₀ = (a₁ + 7d + a₁ + 9d) * 3 / 2 = (2a₁ + 16d) * 3 / 2 = (a₁ + 8d) * 3
По условию эта сумма равна 30.
S₈₋₁₀ = 30
(a₁ + 8d) * 3 = 30 => a₁ + 8d = 10
3.
Имеем систему двух уравнений:
{7a₁ + 21d = 30
{a₁ + 8d = 10
Второе уравнение умножим на (- 7)
{7a₁ + 21d = 30
{a₁ + 8d = 10 | * (-7)
Получим
{7a₁ + 21d = 30
{- 7a₁ - 56d = - 70
Сложив эти уравнения, имеем:
7a₁ + 21d - 7a₁ - 56d = 30 - 70
- 35d = - 40
Сократим на (-5)
7d = 8
d = 8/7 - знаменатель прогрессии
Подставив в уравнение a₁ + 8d = 10 значение d = 8/7, найдём а₁
a₁ + 8 * 8/7 = 10
a₁ = 10 - 64/7 = 70/7 - 64/7 = 6/7
а₁ = 6/7 - первый член прогрессии
4.
Найдём а₂ - второй член данной прогрессии
a₂ = a₁ + d
a₂ = 6/7 + 8/7 = 14/7 = 2
a₂ = 2
ответ: 2