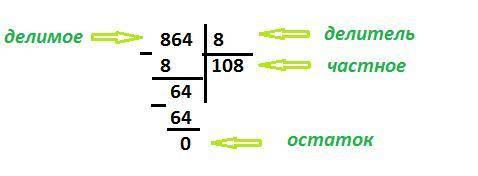
1) Первая цифра 8 делится на 8 нацело, записываем в частное 1.
1 · 8 = 8 → записываем под старшей 8 в числе 864 и вычитаем.
8 - 8 = 0
2) Сносим вниз следующую цифру 6 из числа 864. 6 < 8, на 8 поделить нельзя. Записываем в частное 0.
3) Сносим вниз следующую цифру 4 из числа 864. 64 делится на 8 нацело. Записываем в частное 8.
8 · 8 = 64 → записываем под числом 64 и вычитаем.
64 - 64 = 0
Все цифры числа 864 снесены вниз и поделены, деление закончено. Остаток равен нулю. Частное равно 108.
864 : 8 = 108
Примеры решений задач о выборе шаров
Пример 1. В урне 10 белых и 8 черных шаров. Наудачу отобраны 5 шаров. Найти вероятность того, что среди них окажется ровно 2 белых шара.
Подставляем в формулу (1) значения: K=10, N−K=8, итого N=10+8=18, выбираем n=5 шаров, из них должно быть k=2 белых и соответственно, n−k=5−2=3 черных. Получаем:
P=C210⋅C38C518=45⋅568568=517=0.294.
Пример 2. В урне 5 белых и 5 красных шаров. Какова вероятность вытащить наудачу оба белых шара?
Здесь шары не черные и белые, а красные и белые. Но это совсем не влияет на ход решения и ответ.
Подставляем в формулу (1) значения: K=5 (белых шаров), N−K=5 (красных шаров), итого N=5+5=10 (всего шаров в урне), выбираем n=2 шара, из них должно быть k=2 белых и соответственно, n−k=2−2=0 красных. Получаем:
P=C25⋅C05C210=10⋅145=29=0.222.
Пример 3. В корзине лежат 4 белых и 2 черных шара. Из корзины достали 2 шара. Какова вероятность, что они одного цвета?
Здесь задача немного усложняется, и решим мы ее по шагам. Введем искомое событие
A= (Выбранные шары одного цвета) = (Выбрано или 2 белых, или 2 черных шара).
Представим это событие как сумму двух несовместных событий: A=A1+A2, где
A1= (Выбраны 2 белых шара),
A2= (Выбраны 2 черных шара).
Выпишем значения параметров: K=4 (белых шаров), N−K=2 (черных шаров), итого N=4+2=6 (всего шаров в корзине). Выбираем n=2 шара.
Для события A1 из них должно быть k=2 белых и соответственно, n−k=2−2=0 черных. Получаем:
P(A1)=C24⋅C02C26=6⋅115=25=0.4.
Для события A2 из выбранных шаров должно оказаться k=0 белых и n−k=2 черных. Получаем:
P(A2)=C04⋅C22C26=1⋅115=115.
Тогда вероятность искомого события (вынутые шары одного цвета) есть сумма вероятностей этих событий:
P(A)=P(A1)+P(A2)=25+115=715=0.467.
10 000 000
9000