Пошаговое объяснение:
\ begin {gather} sin \ 2x + sin \ 6x = 0 \\ 2sin \ frac {2x + 6x} {2} cos \ frac {2x-6x} {2} = 0 \\ sin \ 4x \ cos \ 2x = 0 \\ \ left [{{sin \ 4x = O} \ atop {cos \ 2x = 0}} \ right. <=> \ left [{{4x = \ pi k} \ atop {2x = \ frac {\ pi} {2} +2 \ pi n}} \ right. <=> \ left [{{x = \ frac {\ pi k} {4} \ atop {x = \ frac {\ pi} {4} + \ pi n}} \ right. => x = \ dfrac {\ pi m} {4} \\ k \ in Z, \ n \ in Z, \ m \ in Z. \ ||| Ombem: \ \ \ dfrac {\ pi m} {4}; \ \ m \ in Z. \ end {gather}% 3D
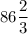
Пошаговое объяснение:
Чтобы найти часть (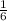 
) числа (120), выраженную дробью, надо это число (120) умножить на дробь:
1) 
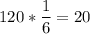(кг) картофеля израсходовали в первый день.
Узнаем, сколько кг картофеля осталось после того, как часть израсходовали в первый день, путем вычитания из исходного количества картофеля части, которую израсходовали в первый день:
2) 120-20 = 100 (кг) картофеля осталось после первого дня.
Узнаем, сколько израсходовали во второй день. Для этого нужно найти часть (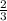 
) от остатка (100):
3) 
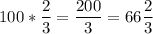(кг) картофеля израсходовали во второй день.
Сложим израсходованное количество картофеля в первый и во второй день, для нахождения количества, которое израсходовали за 2 дня вместе:
4) 
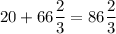(кг) картофеля израсходовали за два дня.
2) 2500, остаток 1.
3) 76, остаток 8.
4) 912, остаток 3.
5) 26, остаток 4.
6) 573, остаток 2.
Примеры настолько простые, что тут даже пояснений не нужно.