153
Пошаговое объяснение:
Из теории графов:
УТВЕРЖДЕНИЕ:
Число всех ребер графа равно полусумме степеней всех вершин графа.
Применительно к нашей задаче
города - вершины графа, соединяющие авиалинии - ребра графа.
Количество ребер выходящих из данной вершины, назыв. её степенью. В нашей задаче все вершины (города) соединены с остальными 17-ю авиалинией. Значит степени каждой вершины =
17.
Итак, по утверждению число всех авиалиний равно полусумме степеней всех вершин графа:
1/2×(18×17)=9×17=153.
P.S. : Можно попробовать проверить справедливость утверждения на малых числах. Пусть будет 3 города, 4 города, 5 городов и т.д.
Пошаговое объяснение:
Всего шаров в каждой урне - n = 10.
Вероятность белого обозначим р = 6/10 = 0.6, тогда вероятность "противного" - чёрного - q = 1 - p = 0.4.
а) Событие описывается как три: из 1 И из 2 И из 3.
Важно; вероятность событий И равна произведению вероятностей каждого.
Р(3 белых) = p³ = 0.6³ = 0.216 - три белых - ответ.
б) Эта задача решается по формуле из п. а)
Q(3 чёрных) = q² = 0.4³ = 0.064 - три чёрных - ответ.
Дополнительно.
А какие другие варианты могут быть?
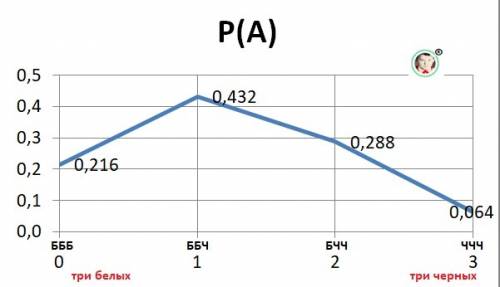
Все возможные - показаны на графике рисунке в приложении.
б наименьшое кратное 12