першым і сапраўдным настаўнікам даніка мальца быў вясковы падполыпчык мікола кужалевіч. аднак жыццё сутыкала героя і з шэрагам іншых настаўнікаў, такіх, як цаба, мар'я, рузя, дулемба. хлопчык, у якога абудзілася пачуццё нацыянальнай самасвядомасці, які адчуў сябе сынам свайго народа, не мог назваць сваімі настаўнікамі паноў цабу, рузю, дулембу, бо тыя ненавідзелі вучняў, абражалі іх, асабліваі пагардліва ставіліся да дзяцей беларусаў.
дарагім чалавекам, сябрам і дарадцам стала для даніка пані мар’я, бо яна адкрывала хлопчыку багацце і разнастайнасць свету, радасць і шчасце вучыцца, харашэць душой, адкрывала беларускую і польскую літаратуру, хараство польскага слова.
данік любуецца знешнім хараством настаўніцы, з захапленнем глядзіць на мілы твар, які абрамляе шапка кучаравых, коратка пастрыжаных валасоў, на чорныя доўгія вейкі, якія прыкрываюць жывыя карыя вочы, на белую зграбную ручку. даніку так хацелася, каб гэтая рука легла яму на галаву. хлопчык захапляецца непасрэднасцю, шчырасцю настаўніцы, яе здольнасцю паспачуваць чужой бядзе, парадавацца поспеху вучня, яму.
пані мар'я любіць сваіх вучняў, падтрымлівае іх стараннасць, карае нядбайнасць, верыць у духоўныя мажлівасці беларускіх дзяцей, у тое, што з цягам часу яны змогуць унесці свой уклад у духоўную скарбніцуі чалавецтва. дзеці таксама любілі сваю «кіраўнічыху», бо яна вылучалася інтэлігентнасцю, дэмакратызмам шчырым жаданнем навучыць, выхаваць, падтрымаць сваіх выхаванцаў.
надеюсь смогла
1) 2√10 см; 2√15 см
2) ∠АОВ=2·∠ACB или 2·arcsin√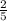
∠АОС=2·∠AВС или 2·arcsin√ .
.
Пошаговое объяснение:
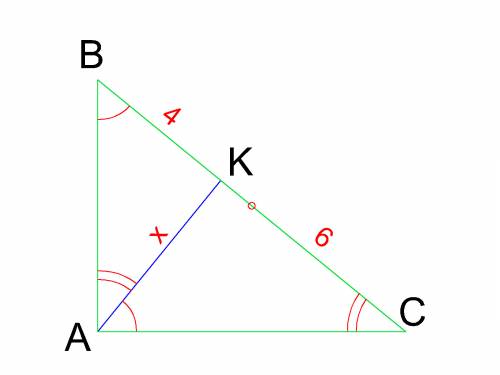
1) Высота, опущенная из вершины прямого угла делит прямоугольник на 2 подобных ему прямоугольника. Это следует из первого признака подобия (равенство двух углов)
Рассмотрим рисунок. Имеем исходный прямоугольный ΔАВС и подобные ему ΔКАС и ΔКВА.
Примем высоту АК за х. Тогда из подобия треугольников получим:
х/4=6/х ⇒ х²=24 ⇒ х=√24.
Из прямоугольных ΔКАС и ΔКВА найдем катеты ΔАВС.
АВ=√(ВК²+АК²)=√(16+24)=2√10 см
АС=√(КС²+АК²)=√(36+24)=2√15 см
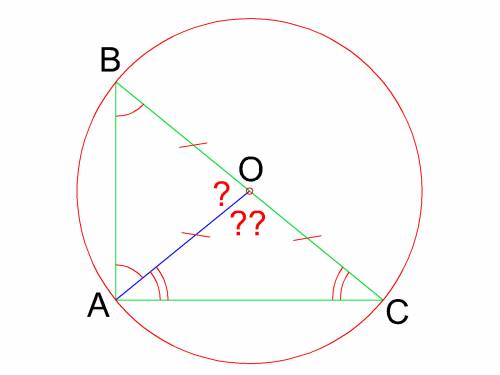
2) Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Пусть т. О - середина гипотенузы ΔАВС. Тогда получаем два равнобедренных ΔАВО и ΔАСО с основаниями АВ и АС соответственно.
Из свойств сегментов окружностей известно, что угол сегмента окружности равен 2·arcsin( с/2R), где с-длина хорды, R-радиус окружности.
Тогда ∠АОВ=2·arcsin( AB/BC) ⇒ ∠АОВ=2·arcsin( sin∠ACB)=2·∠ACB.
Соответственно:
∠АОС=2·arcsin( AС/BC) ⇒ ∠АОС=2·arcsin( sin∠AВС)=2·∠AВС.
Если нужен цифровой ответ, то
∠АОВ=2·∠ACB=2·arcsin( АВ/ВС)= 2·arcsin(2√10/10)=2·arcsin√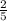
∠АОС=2·arcsin( AС/BC)= 2·arcsin(2√15/10)=2·arcsin√