1.
Пошаговое объяснение:
Пусть n - меньшее из чисел, тогда следующие за ним натуральные числа - (n+1) и (n+2).
Найдём их произведение:
n(n+1)(n+2).
Одно из трёх подряд идущих натуральных чисел кратно трём, т.к. и остатков при делении на 3 всего три: 0,1 и 2.
Хотя бы одно из двух последовательных натуральных чисел чётное, т.к. чётные и нечётные числа чередуются.
Получили, что один из указанных множителей делится на 3 и один из множителей делится на 2, тогда произведение этих натуральных чисел кратно 6.
Дано:
R = 1 см (радиус большого шара)
r = 0,5 см (радиус малых шариков)
π ≈ 3
Найти: n (число полученных малых шариков)
Формула объёма шара: Vш=(4/3)πr³
Так как малые шарики изготовят из того же объёма металла, что был в большом шаре, то просто делим объём большого шара на объём маленького шарика (а затем берём целую часть полученного числа, а дробную- отбрасываем).
Можно решать, сразу выполняя деление (много можно сократить):
Vбольш.ш / Vмал.ш = (4/3)πR³ / ((4/3)πr³) = R³ / r³ = (R / r)³ = (1 / 0,5)³ = 2³ = 8
Результат и так целый, то есть n = 8 (шариков)
Либо, можно отдельно найти объёмы шаров и затем делить:
Vбольш.ш = (4/3)πR³ = (4/3)·3·1³ = 4·1 = 4 см³
Vмал.ш = (4/3)πr³ = (4/3)·3·0,5³ = 4·0,125 = 0,5 см³
Vбольш.ш / Vмал.ш = 4 / 0,5 = 8
n = 8 (шариков)
ответ: n = 8
Рассуждения в разделе "Пошаговое объяснение".
Пошаговое объяснение:Признаки делимости числа на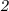 :
:
Число делится на , если его конечная цифра чётная.
, если его конечная цифра чётная.
Пример: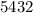 делится на
делится на  , ибо его конечная цифра чётная.
, ибо его конечная цифра чётная.
Признаки делимости числа на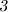 :
:
Число делится на , если сумма его цифр делится на
, если сумма его цифр делится на  .
.
Пример: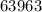 делится на
делится на  , ибо сумма его цифр делится на
, ибо сумма его цифр делится на  .
.
Признаки делимости числа на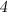 :
:
Число делится на , если его
, если его  последние цифры нули или образуют число, делящиеся на
последние цифры нули или образуют число, делящиеся на  .
.
Пример: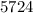 делится на
делится на  , ибо
, ибо  последние цифры (последняя цифра, если число однозначное) образуют число
последние цифры (последняя цифра, если число однозначное) образуют число 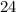 , делящиеся на
, делящиеся на  .
.
Признаки делимости числа на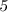 :
:
Число делится на , если его конечная цифра
, если его конечная цифра 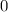 или
или  .
.
Пример: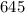 делится на
делится на  , ибо его конечная цифра
, ибо его конечная цифра  .
.
Признаки делимости числа на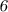 :
:
Число делится на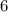 , если конечная цифра чётная и сумма цифр этого числа делится на
, если конечная цифра чётная и сумма цифр этого числа делится на  .
.
Пример: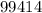 делится на
делится на 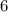 , ибо его конечная цифра
, ибо его конечная цифра  чётная и сумма цифр этого числа делится на
чётная и сумма цифр этого числа делится на  .
.
Признаки делимости числа на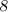 :
:
Число делится на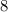 , если
, если  его последние цифры образуют число, делящиеся на
его последние цифры образуют число, делящиеся на 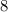 .
.
Пример: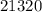 делится на
делится на 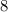 , ибо
, ибо  его последние цифры образуют число
его последние цифры образуют число 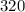 , делящиеся на
, делящиеся на 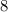 .
.
Признаки делимости числа на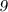 :
:
Число делится на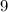 , если сумма его цифр делится на
, если сумма его цифр делится на 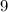 .
.
Пример: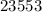 делится на
делится на 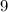 , ибо сумма его цифр делится на
, ибо сумма его цифр делится на 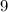 .
.
Признаки делимости числа на :
:
Число делится на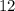 , если оно кратно
, если оно кратно  и
и  .
.
Пример: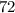 делится на
делится на 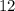 , ибо оно кратно
, ибо оно кратно  и
и  .
.
Признаки делимости числа на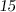 :
:
Число делится на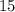 , если его конечная цифра
, если его конечная цифра 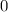 или
или  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
Пример: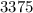 делится на
делится на 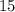 , ибо его конечная цифра
, ибо его конечная цифра  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
------------------------------------------------------------------------------------------------
Какие из чисел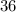 делится на
делится на 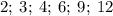 , ибо его конечная цифра чётная, сумма цифр этого числа делится на
, ибо его конечная цифра чётная, сумма цифр этого числа делится на  и
и 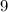 , оно кратно
, оно кратно  и
и  , его
, его  последние цифры образуют число, делящиеся на
последние цифры образуют число, делящиеся на  .
.
Какие из чиселСправедливо неравенство: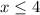 .
.
Числа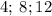 кратны
кратны  , ибо последняя цифра
, ибо последняя цифра 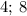 делится/
делится/ последние цифры
последние цифры 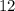 делятся на
делятся на  .
.
Какие из чисел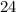 и
и 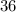 одновременно делятся на
одновременно делятся на 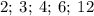 , ибо их конечные цифры чётные, суммы цифр этих чисел делятся на
, ибо их конечные цифры чётные, суммы цифр этих чисел делятся на  , их
, их  последние цифры образуют числа, делящиеся на
последние цифры образуют числа, делящиеся на  .
.
Какие из чиселТребования к заданию: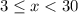 , где
, где  - искомые числа. Число
- искомые числа. Число  уже не подходит.
уже не подходит.
Числа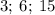 являются делителями
являются делителями 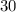 и кратны
и кратны  , ибо сумма цифр числа
, ибо сумма цифр числа 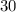 делится на
делится на  , последняя цифра
, последняя цифра 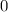 и она чётная.
и она чётная.