Разряды нумеруются справа – налево, с наименьшего.
Первый разряд – единицы.
Второй разряд – десятки.
Третий разряд – сотни.
Четвёртый – тысячи.
1) 4 единицы 2-ого разряда, 5 единиц 3-го разряда – это 540
2) 4 единицы 1-го разряда, 5 единиц 2-го разряда, 6 единиц 3-го разряда – это 654
3) 4 единицы 1-го разряда, 5 единиц 2-го разряда – это 54
4) 4 единицы 1-го разряда, 5 единиц 3-го разряда – это 504
5) 3 единицы 1-го разряда,4 единицы 2-го разряда, 5 единиц 3-го разряда – это 543
2х+3у-7=0
Пошаговое объяснение:
1) Нужно найти координаты вершины А. Очевидно, что она лежит на пересечении прямых АВ и АС, т.е. у этой точки значения у и х будут принадлежать области значений и определения обеих функций. Другими словами, нам нужно решить систему их уравнений.
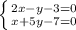
Из уравнения АВ: у=2х-3,
подставляем в уравнение АС: х+5·(2х-3)-7=0
х+10х-15-7=0
11х=22
х=2
у=2·2-3=1
Итого, имеем координаты вершины А(2;1).
2) Нужно составить общее уравнение прямой а, проходящей через точку А и перпендикулярную прямой ВС.
Так как прямая а перпендикулярна прямой ВС, то направляющий вектор прямой а есть нормальный вектор заданной прямой 3x-2y+13=0, то есть, направляющий вектор прямой а имеет координаты (3;-2).
Теперь мы можем записать каноническое уравнение прямой а на плоскости, так как знаем координаты точки А, через которую проходит прямая а, и координаты направляющего вектора прямой а:
=
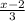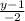. (Здесь в числителях задействованы координаты точки А, в знаменателях - координаты напрявляющего вектора)
От полученного канонического уравнения прямой a перейдем к общему уравнению прямой:
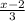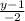= ⇒ -2·(х-2)=3·(у-1) ⇒ 2х+3у-7=0.
ответ: уравнение высоты, проведенной через вершину A 2х+3у-7=0
1й разряд - это единицы
2й разряд - десятки
3й разряд - сотни
4 единицы 2 разряда 5 единиц 3 разряда = 540
4 единицы 1 разряда ,5 единиц 2 разряда, 6 единиц 3 разряда = 654
4 единицы 1 разряда, 5 единиц 2 разряда = 54
4 единицы 1 разряда, 5 единиц 3 разряда = 504
3 единицы 1 разряда ,4 единицы 2 разряда, 5 единиц 3 разряда = 543