Дана функция у = 2х² - х⁴.
1.Область определения функции: x ∈ R, или -∞ < x < ∞.
2. Нули функции. Точки пересечения графика функции с осью ОХ.
2х² - х⁴ = 0, х²(2 - х²) = 0. Тогда х² = 0 и (или) 2 - х² = 0.
x₁ = 0.
x₂ = √2.
х₃ = -√2.
Точки пересечения графика функции с осью ОУ при х = 0 ⇒ у = 0.
3. Промежутки знакопостоянства функции.
Для нахождения промежутков знакопостоянства функции y=f(x) надо решить неравенства f(x)>0, f(x)<0.
По пункту 2 имеем 4 промежутка значений аргумента, в которых функция сохраняет знак:
(−∞;−√2), (−√2;0), (0;√2), (√2;+∞).
Для того, чтобы определить знак функции на каждом из этих промежутков, надо найти значение функции в произвольной точке из каждого промежутка. Точки выбираются из соображений удобства вычислений.
x = -2 -1 1 2
y = -8 1 1 -8.
В промежутках (−∞;−√2) и (√2;+∞) функция принимает отрицательные значения, в промежутках (−√2;0) и (0;√2) функция принимает положительные значения.
4. Симметрия графика (чётность или нечётность функции).
Проверим функци чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
- x^{4} + 2 x^{2} = - x^{4} + 2 x^{2}
- Да
- x^{4} + 2 x^{2} = - -1 x^{4} - 2 x^{2}
- Нет
Значит, функция является чётной.
5. Периодичность графика - нет.
6.Точки разрыва, поведение функции в окрестностях точек разрыва, вертикальные асимптоты - нет.
7. Интервалы монотонности функции, точки экстремумов, значения функции в точках экстремумов.
Находим производную заданной функции:
y' = 4x - 4x³.
Приравниваем производную нулю: 4x - 4x³ = 4x(1 - x²) = 0,
4x = 0, x = 0.
x² = 1, х = 1, x = -1.
Критических точек три: х = 0, х = 1, x = -1.
Находим значения производной левее и правее от критических.
x = -2 -1 -0.5 0 0.5 1 2
y' = 24 0 -1.5 0 1.5 0 -24.
Где производная положительна - функция возрастает, где отрицательна - там убывает.
Убывает на промежутках (-oo, -1] U [0, oo).
Возрастает на промежутках (-oo, 0] U [1, oo).
8. Интервалы выпуклости, точки перегиба.
Найдем точки перегибов, для этого надо решить уравнение
\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0.
Вторая производная 4 \left(- 3 x^{2} + 1\right) = 0.
Решаем это уравнение.
Корни этого уравнения:
x_{1} = - \frac{\sqrt{3}}{3}
x_{2} = \frac{\sqrt{3}}{3}
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках [-sqrt(3)/3, sqrt(3)/3].
Выпуклая на промежутках (-oo, -sqrt(3)/3] U [sqrt(3)/3, oo).
9. Поведение функции в бесконечности. Наклонные (в частности, горизонтальные) асимптоты - нет.
10. Дополнительные точки, позволяющие более точно построить график.
11. Построение графика функции - дан в приложении.
1) 2√10 см; 2√15 см
2) ∠АОВ=2·∠ACB или 2·arcsin√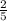
∠АОС=2·∠AВС или 2·arcsin√ .
.
Пошаговое объяснение:
1) Высота, опущенная из вершины прямого угла делит прямоугольник на 2 подобных ему прямоугольника. Это следует из первого признака подобия (равенство двух углов)
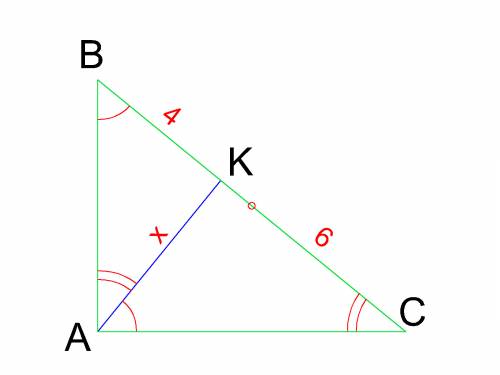
Рассмотрим рисунок. Имеем исходный прямоугольный ΔАВС и подобные ему ΔКАС и ΔКВА.
Примем высоту АК за х. Тогда из подобия треугольников получим:
х/4=6/х ⇒ х²=24 ⇒ х=√24.
Из прямоугольных ΔКАС и ΔКВА найдем катеты ΔАВС.
АВ=√(ВК²+АК²)=√(16+24)=2√10 см
АС=√(КС²+АК²)=√(36+24)=2√15 см
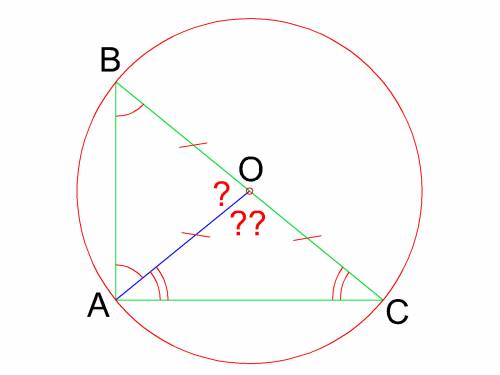
2) Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Пусть т. О - середина гипотенузы ΔАВС. Тогда получаем два равнобедренных ΔАВО и ΔАСО с основаниями АВ и АС соответственно.
Из свойств сегментов окружностей известно, что угол сегмента окружности равен 2·arcsin( с/2R), где с-длина хорды, R-радиус окружности.
Тогда ∠АОВ=2·arcsin( AB/BC) ⇒ ∠АОВ=2·arcsin( sin∠ACB)=2·∠ACB.
Соответственно:
∠АОС=2·arcsin( AС/BC) ⇒ ∠АОС=2·arcsin( sin∠AВС)=2·∠AВС.
Если нужен цифровой ответ, то
∠АОВ=2·∠ACB=2·arcsin( АВ/ВС)= 2·arcsin(2√10/10)=2·arcsin√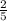
∠АОС=2·arcsin( AС/BC)= 2·arcsin(2√15/10)=2·arcsin√
×=100-48
х=52