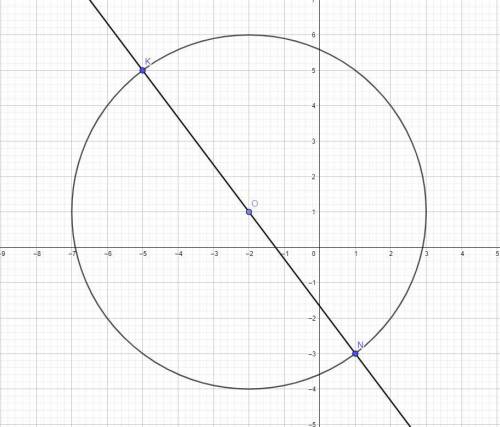
1. 1 2/5
2. а) 8b - 2
б) 16а - 4
в) 9 - 2а
3. 2
Пошаговое объяснение:
1. 4x+3y/4x-3y, при x=-3/4,y=-1/6
4 * (-3/4) + 3 * (-1/6)) : ((4 * (-3/4) - 3 * (-1/6) =
(-3 - 1/2) : (-3 +1/2) = -3 1/2 : -2 1/2 = 1 2/5
2. а) -2(2b – 3) + 4(3b – 2) = -4b + 6 + 12b – 8 = 8b - 2
б) 15a - (а + 3) + (2а – 1) = 15а - а - 3 + 2а - 1 = 16а - 4
в) 5а – (6а – (7а – (8а - 9))) = 5а – (6а – (7а - 8а + 9) =
5а – (6а – (- 1а +9)) = 5а – (6а + 1а - 9) = 5а - 6а - 1а + 9 = 9 - 2а
3. -2(3,5y – 2,5) + 4,5y- 1, при y=4/5
-2(3 1/2 * 4/5 – 2,5) + 4,5 * 4/5 - 1 = -2 * (2,8 - 2,5) + 3,6 - 1 =
-5,6 + 5 + 2,6 = -0,6 + 2,6 = 2
Координати центра кола: (1; -2).
Довжина радіуса кола: 5 одиниць.
Рівняння кола: (x + 2)² + (y - 1)² = 25
Рівняння прямої: y = (-4x - 5) / 3
Пошаговое объяснение:
Побудуємо точки K(-5; 5) i N(1; -3) на координатній площині.
1) знайдемо радіус кола.
Радіусом кола буде середина вектора KN:
X(c) = (-5 + 1) / 2 = -2
Y(c) = (5 + (-3)) / 2 = (5 - 3) / 2 = 2 / 2 = 1
Отже, середина вектора KN знаходиться у точці: O(1; -2).
Це буде радіусом даного кола, адже пряма проходить центр.
2) будуємо коло з центром у точці О(1; -2), на якому лежатимуть дві точки: K(-5; 5) i N(1; -3) *на фото
3) знайдемо довжину радіуса кола:
Знайдемо модуль вектора та поділимо його на 2 (r = d/2):
__ _________ ____
KN = (1 - (-5); -3 - 5) = (6; -8)
r = | KN | / 2 = √(36 + 64) / 2 = √100 / 2 = 10 / 2 = 5 (одиниць)
4) запишемо рівняння кола:
(x - x₀)² + (y - y₀)² = R²
(x + 2)² + (y - 1)² = 25
5) запишемо рівняння прямої:
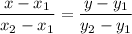
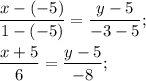
-8(x + 5) = 6(y - 5)
-8x - 40 = 6y - 30
6y + 8x + 10 = 0
6y = -8x - 10
y = (-4x - 5) / 3